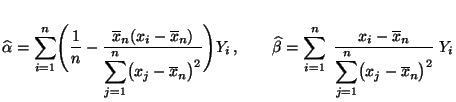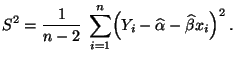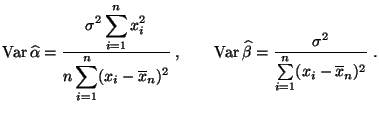Next: Normalverteilte Störgrößen
Up: Einfache lineare Regression
Previous: Einfache lineare Regression
Contents
Kleinste-Quadrate-Schätzer
- Zur Erinnerung: Bei der Konstruktion von Schätzern für
(reellwertige) Modellparameter geht man wie folgt vor.
- Man betrachtet eine Abbildung
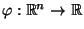 , die den
beobachteten Daten
, die den
beobachteten Daten
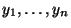 , d.h. jeder Realisierung
, d.h. jeder Realisierung
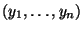 der Zufallsstichprobe
der Zufallsstichprobe
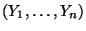 , den
Schätzwert
, den
Schätzwert
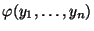 zuordnet.
zuordnet.
- Der zugehörige Schätzer ist dann die (reellwertige)
Zufallsvariable
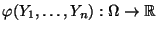 , die sich
ergibt, wenn die Abbildungen
, die sich
ergibt, wenn die Abbildungen
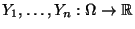 und
und
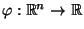 nacheinander ausgeführt werden.
nacheinander ausgeführt werden.
- Zur Vereinfachung der Schreibweise werden wir gelegentlich sowohl
den Schätzer als auch den (aus den jeweils beobachteten Daten
bestimmten) Schätzwert mit
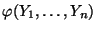 bezeichnen.
bezeichnen.
- Mit der bereits in Abschnitt 2.5.2 diskutierten
Methode der kleinsten Quadrate erhalten wir die folgenden Schätzer
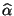 ,
,
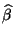 bzw.
bzw.
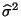 für die
Modellparameter
für die
Modellparameter 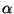 ,
, 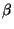 und
und 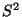 :
:
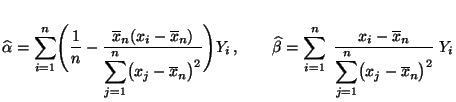 |
(4) |
- und
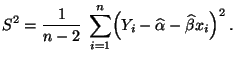 |
(5) |
- Hieraus ergibt sich für die Erwartungswerte dieser Schätzer, dass
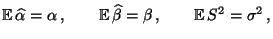 |
(6) |
- d.h., die Modellparameter
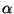 ,
, 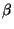 bzw.
bzw. 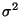 werden
im Mittel durch
werden
im Mittel durch
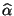 ,
,
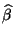 bzw.
bzw. 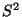 ,,richtig'' geschätzt.
,,richtig'' geschätzt.
- Mit anderen Worten:
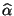 ,
,
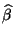 bzw.
bzw. 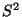 sind sogenannte erwartungstreue Schätzer für
sind sogenannte erwartungstreue Schätzer für 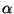 ,
,
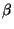 bzw.
bzw. 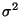 .
.
- Für die Varianzen der Schätzer
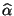 und
und
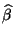 gilt:
gilt:
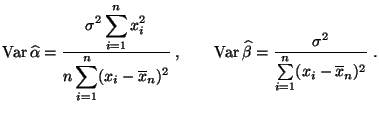 |
(7) |
- Beachte




Next: Normalverteilte Störgrößen
Up: Einfache lineare Regression
Previous: Einfache lineare Regression
Contents
Hendrik Schmidt
2003-07-21
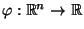 , die den
beobachteten Daten
, die den
beobachteten Daten
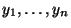 , d.h. jeder Realisierung
, d.h. jeder Realisierung
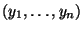 der Zufallsstichprobe
der Zufallsstichprobe
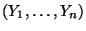 , den
Schätzwert
, den
Schätzwert
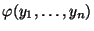 zuordnet.
zuordnet.
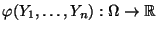 , die sich
ergibt, wenn die Abbildungen
, die sich
ergibt, wenn die Abbildungen
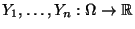 und
und
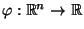 nacheinander ausgeführt werden.
nacheinander ausgeführt werden.
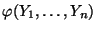 bezeichnen.
bezeichnen.
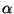 ,
, 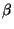 bzw.
bzw. 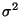 werden
im Mittel durch
werden
im Mittel durch
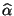 ,
,
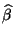 bzw.
bzw. 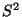 ,,richtig'' geschätzt.
,,richtig'' geschätzt.
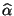 ,
,
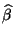 bzw.
bzw. 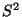 sind sogenannte erwartungstreue Schätzer für
sind sogenannte erwartungstreue Schätzer für 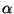 ,
,
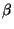 bzw.
bzw. 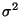 .
.
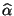 und
und
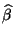 für
für 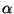 bzw.
bzw. 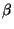 sind sogenannte lineare Schätzer, d.h., sie sind Linearkombinationen der
Stichprobenvariablen
sind sogenannte lineare Schätzer, d.h., sie sind Linearkombinationen der
Stichprobenvariablen
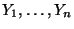 .
.
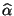 und
und
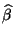 sind im
allgemeinen nicht unabhängig, denn für die Kovarianz
sind im
allgemeinen nicht unabhängig, denn für die Kovarianz
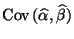 von
von
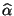 und
und
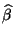 gilt:
gilt: