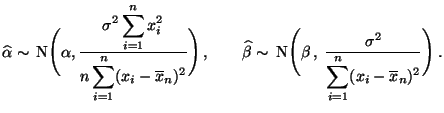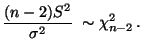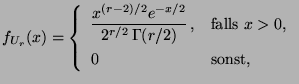Next: t-Tests für Regressionskonstante und
Up: Einfache lineare Regression
Previous: Kleinste-Quadrate-Schätzer
Contents
Normalverteilte Störgrößen
- Um Aussagen über die Verteilungen der in (4) bzw.
(5)
betrachteten Kleinste-Quadrate-Schätzer
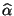 ,
,
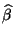 und
und 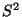 machen zu können, benötigen wir
Verteilungsannahmen über die (zufälligen) Störgrößen
machen zu können, benötigen wir
Verteilungsannahmen über die (zufälligen) Störgrößen
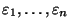 .
.
- Zusätzlich zu den Modellannahmen, die bisher in
Abschnitt 3.1 gemacht wurden, setzen wir deshalb von
nun an voraus, dass
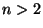 und dass die (unabhängigen und identisch
verteilten) Störgrößen
und dass die (unabhängigen und identisch
verteilten) Störgrößen
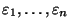 normalverteilt sind.
normalverteilt sind.
- Zur Erinnerung: Seien
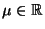 und
und
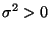 beliebige,
jedoch fest vorgegebene Zahlen. Man sagt, dass die Zufallsvariable
beliebige,
jedoch fest vorgegebene Zahlen. Man sagt, dass die Zufallsvariable
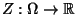 normalverteilt ist mit dem Erwartungswert
normalverteilt ist mit dem Erwartungswert
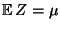 und der Varianz
und der Varianz
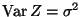 (und verwendet dann
die Schreibweise
(und verwendet dann
die Schreibweise 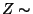 N
N
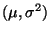 ), falls die Dichte von
), falls die Dichte von
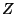 gegeben ist durch
mit der graphischen Darstellung:
gegeben ist durch
mit der graphischen Darstellung:
- Wegen (1) gilt dann
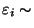 N
N
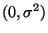 ,
d.h., der Erwartungswert
,
d.h., der Erwartungswert
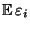 der normalverteilten Störgröße
der normalverteilten Störgröße
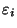 ist 0 und die Varianz
ist 0 und die Varianz
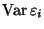 von
von
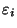 ist
ist
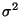 für jedes
für jedes
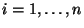 .
.
- Mit anderen Worten: Die Wahrscheinlichkeitsdichte
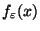 der Zufallsvariablen
der Zufallsvariablen
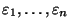 ist gegeben
durch
ist gegeben
durch
- Wegen der Invarianzeigenschaften der Normalverteilung unter
Linear-Transformation folgt hieraus außerdem, dass die
(unabhängigen, jedoch im allgemeinen nicht identisch verteilten)
Zielvariablen
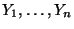 ebenfalls normalverteilt sind,
wobei
ebenfalls normalverteilt sind,
wobei
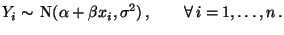 |
(9) |
- Weil die Kleinste-Quadrate-Schätzer
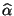 und
und
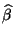 Linearkombinationen der unabhängigen und
normalverteilten Zielvariablen
Linearkombinationen der unabhängigen und
normalverteilten Zielvariablen
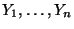 sind, ergibt sich
nun aus (4) und (9) (wegen der
sogenannten Faltungsstabilität der Normalverteilung),
sind, ergibt sich
nun aus (4) und (9) (wegen der
sogenannten Faltungsstabilität der Normalverteilung),
- Zur Erinnerung: Sei
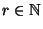 eine beliebige natürliche Zahl, und
seien
eine beliebige natürliche Zahl, und
seien
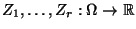 unabhängige und
N
unabhängige und
N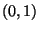 -verteilte Zufallsvariablen.
-verteilte Zufallsvariablen.




Next: t-Tests für Regressionskonstante und
Up: Einfache lineare Regression
Previous: Kleinste-Quadrate-Schätzer
Contents
Hendrik Schmidt
2003-07-21
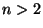 und dass die (unabhängigen und identisch
verteilten) Störgrößen
und dass die (unabhängigen und identisch
verteilten) Störgrößen
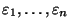 normalverteilt sind.
normalverteilt sind.
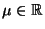 und
und
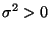 beliebige,
jedoch fest vorgegebene Zahlen. Man sagt, dass die Zufallsvariable
beliebige,
jedoch fest vorgegebene Zahlen. Man sagt, dass die Zufallsvariable
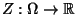 normalverteilt ist mit dem Erwartungswert
normalverteilt ist mit dem Erwartungswert
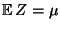 und der Varianz
und der Varianz
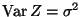 (und verwendet dann
die Schreibweise
(und verwendet dann
die Schreibweise 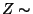 N
N
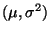 ), falls die Dichte von
), falls die Dichte von
 gegeben ist durch
mit der graphischen Darstellung:
gegeben ist durch
mit der graphischen Darstellung: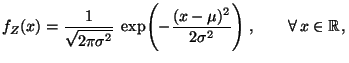
![\includegraphics[width=8cm]{wista_pdfnormal.eps}](img549.png)
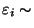 N
N
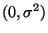 ,
d.h., der Erwartungswert
,
d.h., der Erwartungswert
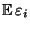 der normalverteilten Störgröße
der normalverteilten Störgröße
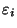 ist 0 und die Varianz
ist 0 und die Varianz
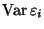 von
von
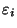 ist
ist
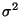 für jedes
für jedes
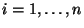 .
.
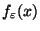 der Zufallsvariablen
der Zufallsvariablen
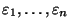 ist gegeben
durch
ist gegeben
durch
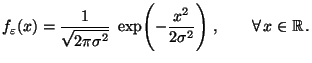
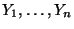 ebenfalls normalverteilt sind,
wobei
ebenfalls normalverteilt sind,
wobei
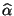 und
und
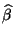 normalverteilt sind, wobei
normalverteilt sind, wobei
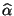 und
und
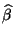 gebildete Zufallsvektor
gebildete Zufallsvektor
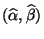 unabhängig ist von dem
Kleinste-Quadrate-Schätzer
unabhängig ist von dem
Kleinste-Quadrate-Schätzer 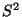 ,
,
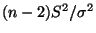 eine sogenannte
eine sogenannte
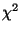 -Verteilung mit
-Verteilung mit  Freiheitsgraden hat,
d.h.,
Freiheitsgraden hat,
d.h.,
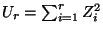 eine
eine 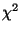 -Verteilung mit
-Verteilung mit 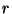 Freiheitsgraden hat.
(Schreibweise:
Freiheitsgraden hat.
(Schreibweise:
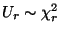 ).
).
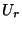 ist gegeben durch
ist gegeben durch
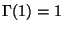 ,
,
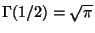 und
und
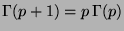 , mit der graphischen Darstellung:
, mit der graphischen Darstellung:
![\includegraphics[width=9cm]{wista_pdfchisquare.eps}](img573.png)
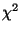 -Verteilungen bilden eine Klasse von sogenannten statistischen Prüfverteilungen, die bei der Konstruktion von
Signifikanztests bzw. Konfidenzintervallen nützlich sind, vgl. die
nachfolgenden Abschnitte 3.1.3-3.1.6.
-Verteilungen bilden eine Klasse von sogenannten statistischen Prüfverteilungen, die bei der Konstruktion von
Signifikanztests bzw. Konfidenzintervallen nützlich sind, vgl. die
nachfolgenden Abschnitte 3.1.3-3.1.6.