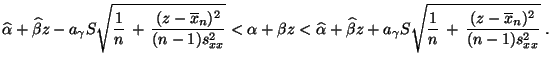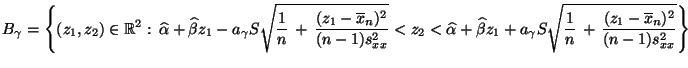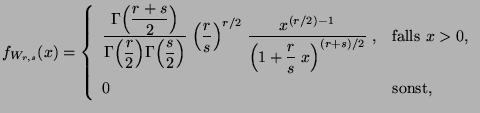- Auf ähnliche Weise wie in Abschnitt 3.1.4 kann man
sogenannte simultane Konfidenzbereiche zum Niveau
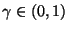
- gleichzeitig für mehrere erwartete Zielwerte
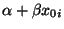 ,
,
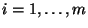 angeben, die vorgegebenen (Ausgangs-)
Werten
angeben, die vorgegebenen (Ausgangs-)
Werten
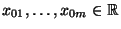 entsprechen.
entsprechen.
- Dabei ist erneut der Fall
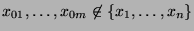 von besonderem
Interesse, d.h., wenn an den Stellen
von besonderem
Interesse, d.h., wenn an den Stellen
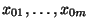 keine
Daten erhoben werden.
keine
Daten erhoben werden.
- Man kann nämlich zeigen, dass die Wahrscheinlichkeit mindestens
gleich
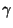 ist, dass
ist, dass
gleichzeitig für jedes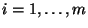 gilt, wobei
gilt, wobei
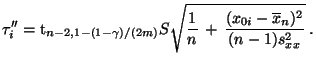
- gleichzeitig für mehrere erwartete Zielwerte
- Das kartesische Produkt
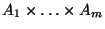 der
der 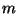 Intervalle
Intervalle
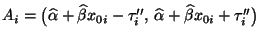 in (30) heißt
simultaner Konfidenzbereich für den Vektor
in (30) heißt
simultaner Konfidenzbereich für den Vektor
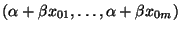 .
.
- Wir gehen nun noch einen Schritt weiter als in (30)
und fragen,
- ob es eine Zahl
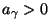 gibt, so dass die Wahrscheinlichkeit
mindestens gleich
gibt, so dass die Wahrscheinlichkeit
mindestens gleich 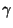 ist, dass gleichzeitig für jedes
ist, dass gleichzeitig für jedes
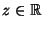
- Die Menge
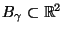 mit
mit
heißt dann Konfidenzband zum Niveau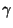 für die
Regressionsgerade
für die
Regressionsgerade
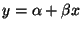 .
.
- ob es eine Zahl
- Bei der Lösung dieser Fragestellung ist die F-Verteilung nützlich,
die ebenfalls eine Klasse von statistischen Prüfverteilungen
bildet.
- Zur Erinnerung: Seien
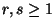 beliebige natürliche Zahlen, und
seien
beliebige natürliche Zahlen, und
seien
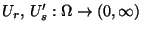 unabhängige
unabhängige
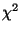 -verteilte Zufallsvariablen mit
-verteilte Zufallsvariablen mit
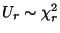 und
und
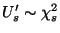 .
.
- Man sagt dann, dass die Zufallsvariable
F-verteilt ist mit
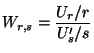
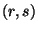 Freiheitsgraden. (Schreibweise:
Freiheitsgraden. (Schreibweise:
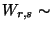 F
F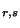 )
)
- Die Dichte von
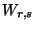 ist gegeben durch
ist gegeben durch
mit der graphischen Darstellung:
![\includegraphics[width=8cm]{wista_pdfF.eps}](img723.png)
- Zur Erinnerung: Seien
- Man kann zeigen, dass durch die in
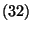 definierte Menge
definierte Menge
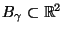 ein Konfidenzband
zum Niveau
ein Konfidenzband
zum Niveau 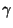 für die Regressionsgerade
für die Regressionsgerade
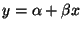 gegeben ist, wenn
gegeben ist, wenn 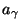 wie folgt gewählt wird:
wie folgt gewählt wird:
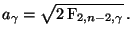
- Beachte
- Es ist klar, dass t
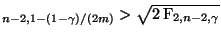 für jedes hinreichend große
für jedes hinreichend große 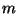 gilt .
gilt .
- Hieraus folgt, dass der simultane Konfidenzbereich, der in
(30) betrachtet wurde, für große
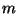 größer
ist als der simultane Konfidenzbereich, der sich aus dem in
(31) betrachteten Konfidenzband ergibt.
größer
ist als der simultane Konfidenzbereich, der sich aus dem in
(31) betrachteten Konfidenzband ergibt.
- Auf den ersten Blick scheint dies ein Widerspruch zu sein, weil in
(31) die Überdeckungseigenschaft für alle
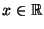 gefordert wird, während diese Eigenschaft in
(30) nur für endlich viele Ausgangswerte
gefordert wird, während diese Eigenschaft in
(30) nur für endlich viele Ausgangswerte
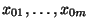 betrachtet wird.
betrachtet wird.
- Der Grund, dass (31) für große
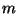 zu kleineren
(d.h. besseren) simultanen Konfidenzbereichen führt, besteht
darin, dass bei der Herleitung von (30) die
sogenannte Bonferroni-Ungleichung der
Wahrscheinlichkeitsrechnung verwendet wird, die für große
zu kleineren
(d.h. besseren) simultanen Konfidenzbereichen führt, besteht
darin, dass bei der Herleitung von (30) die
sogenannte Bonferroni-Ungleichung der
Wahrscheinlichkeitsrechnung verwendet wird, die für große 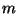 nur
eine sehr ungenaue untere Schranke für die Wahrscheinlichkeit
nur
eine sehr ungenaue untere Schranke für die Wahrscheinlichkeit
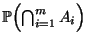 liefert, wobei
liefert, wobei

- Es ist klar, dass t
- Beispiele
- Aus den Daten über Weglängen und Lieferzeiten ergibt sich das
folgende Konfidenzband zum Niveau
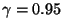 , das an der
Stelle
, das an der
Stelle
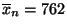 die kleinste Breite aufweist:
die kleinste Breite aufweist:
![\includegraphics[width=7cm]{wista_confidencespedition_1.eps}](img732.png)
- Auf ähnliche Weise ergibt sich aus den Daten über die beiden
Merkmale ,,Geburtsgewicht'' und ,,Gewichtszunahme'' das folgende
Konfidenzband zum Niveau
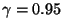 , das an der Stelle
, das an der Stelle
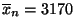 die kleinste Breite aufweist:
die kleinste Breite aufweist:
![\includegraphics[width=7cm]{wista_confidencegebgewicht_1.eps}](img734.png)
- Aus den Daten über Weglängen und Lieferzeiten ergibt sich das
folgende Konfidenzband zum Niveau