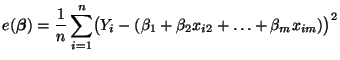Next: t-Tests und Konfidenzintervalle für
Up: Multiple lineare Regression
Previous: Kleinste-Quadrate-Schätzer bei zwei Einflussfaktoren
Contents
Vektor- bzw. Matrixschreibweise
- Wir kehren nun zu dem (allgemeinen) multiplen linearen
Regressionmodell mit einer beliebigen Anzahl
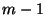 von
Einflussfaktoren zurück, das bereits in
Abschnitt 3.3.1 betrachtet wurde.
von
Einflussfaktoren zurück, das bereits in
Abschnitt 3.3.1 betrachtet wurde.
- Ähnlich wie bei der Herleitung von (57) (d.h. bei
der Lösung des entsprechenden Minimierungsproblems im Fall zweier
Einflussfaktoren) kann man zeigen, dass für eine beliebige Anzahl
von Einflussfaktoren
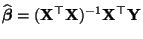 |
(64) |
- das (eindeutig bestimmte) Minimum des in (63)
betrachteten Abweichungsmßes ist,
- wobei
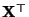 die transponierte
die transponierte 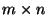 Matrix
bezeichnet, die sich durch Vertauschung der Zeilen und Spalten von
Matrix
bezeichnet, die sich durch Vertauschung der Zeilen und Spalten von
 ergibt,
ergibt,
- und
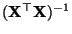 die inverse Matrix von
die inverse Matrix von
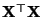 ist.
ist.
- Beachte
- Der Rang
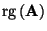 einer Matrix
einer Matrix
 ist die
maximale Anzahl der linear unabhängigen Zeilenvektoren (bzw.
Spaltenvektoren) von
ist die
maximale Anzahl der linear unabhängigen Zeilenvektoren (bzw.
Spaltenvektoren) von
 .
.
- Zur Erinnerung: Die Vektoren
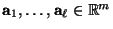 heißen linear abhängig, falls es reelle Zahlen
heißen linear abhängig, falls es reelle Zahlen
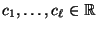 gibt, die nicht alle gleich Null sind,
so dass
gibt, die nicht alle gleich Null sind,
so dass
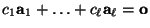 . Anderenfalls
heißen die Vektoren
. Anderenfalls
heißen die Vektoren
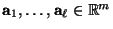 linear unabhängig.
linear unabhängig.
- Weil wir voraussetzen, dass die Designmatrix
 vollen
(Spalten-) Rang
vollen
(Spalten-) Rang
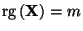 hat, ist die symmetrische
hat, ist die symmetrische 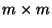 Matrix
Matrix
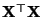 regulär, d.h., es gilt
regulär, d.h., es gilt
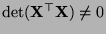 .
.
- Somit ist
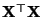 auch invertierbar, d.h., es gibt
eine (eindeutig bestimmte)
auch invertierbar, d.h., es gibt
eine (eindeutig bestimmte) 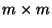 Matrix
Matrix
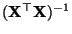 , so dass
wobei
, so dass
wobei
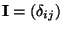 die
die 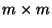 -dimensionale Einheitsmatrix bezeichnet mit
-dimensionale Einheitsmatrix bezeichnet mit
- Beachte
- Der in (64) gegebene Kleinste-Quadrate-Schätzer
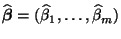 für
den Parametervektor
für
den Parametervektor
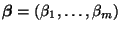 ist ein
sogenannter linearer Schätzer, d.h.,
ist ein
sogenannter linearer Schätzer, d.h.,
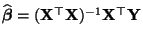 ist eine
lineare Funktion der Zufallsstichprobe
ist eine
lineare Funktion der Zufallsstichprobe
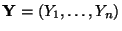 .
.
- Der Schätzer
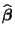 hat die folgenden Güteeigenschaften:
hat die folgenden Güteeigenschaften:
- Es gilt
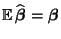 für jedes
für jedes
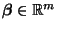 , d.h.,
, d.h.,
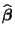 ist erwartungstreu.
ist erwartungstreu.
- Für jeden anderen linaren erwartungstreuen Schätzer
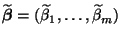 für
für
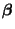 gilt
gilt
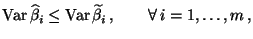 |
(65) |
wobei die Gleichheit in
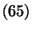 genau dann für jedes
genau dann für jedes
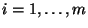 gilt, wenn
gilt, wenn
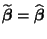 ,
d.h.,
,
d.h.,
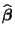 ist bester linearer
erwartungstreuer Schätzer für
ist bester linearer
erwartungstreuer Schätzer für
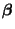 .
.
- Die (zufällige) Abbildung
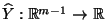 mit
mit
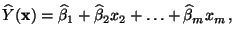 |
(66) |
die jedem Vektor
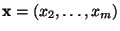 von Werten der
Einflussfaktoren die Zufallsvariable
von Werten der
Einflussfaktoren die Zufallsvariable
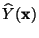 zuordnet,
heißt empirische Regressionshyperebene.
zuordnet,
heißt empirische Regressionshyperebene.
- Außerdem kann man in Verallgemeinerung von (62)
zeigen, dass die ,,Reststreueung''
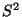 um die empirische
Regressionshyperebene, die gegeben ist durch
um die empirische
Regressionshyperebene, die gegeben ist durch
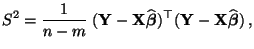 |
(67) |
ein erwartungstreuer Schätzer für 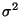 ist, d.h., es gilt
ist, d.h., es gilt
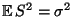 .
.




Next: t-Tests und Konfidenzintervalle für
Up: Multiple lineare Regression
Previous: Kleinste-Quadrate-Schätzer bei zwei Einflussfaktoren
Contents
Hendrik Schmidt
2003-07-21
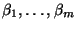 mit der Methode der kleinsten Quadrate
aus den beobachteten Daten
mit der Methode der kleinsten Quadrate
aus den beobachteten Daten
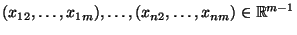 und
und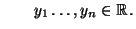
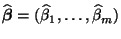 bestimmt werden, so dass der mittlere quadratische Fehler
bestimmt werden, so dass der mittlere quadratische Fehler
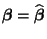 minimal wird, wobei wir
voraussetzen, dass
minimal wird, wobei wir
voraussetzen, dass  und dass der Rang der Matrix
und dass der Rang der Matrix
 gleich
gleich 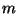 ist.
ist.
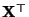 die transponierte
die transponierte 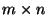 Matrix
bezeichnet, die sich durch Vertauschung der Zeilen und Spalten von
Matrix
bezeichnet, die sich durch Vertauschung der Zeilen und Spalten von
 ergibt,
ergibt,
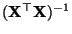 die inverse Matrix von
die inverse Matrix von
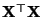 ist.
ist.
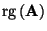 einer Matrix
einer Matrix
 ist die
maximale Anzahl der linear unabhängigen Zeilenvektoren (bzw.
Spaltenvektoren) von
ist die
maximale Anzahl der linear unabhängigen Zeilenvektoren (bzw.
Spaltenvektoren) von
 .
.
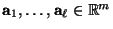 heißen linear abhängig, falls es reelle Zahlen
heißen linear abhängig, falls es reelle Zahlen
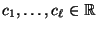 gibt, die nicht alle gleich Null sind,
so dass
gibt, die nicht alle gleich Null sind,
so dass
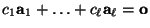 . Anderenfalls
heißen die Vektoren
. Anderenfalls
heißen die Vektoren
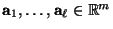 linear unabhängig.
linear unabhängig.
 vollen
(Spalten-) Rang
vollen
(Spalten-) Rang
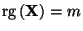 hat, ist die symmetrische
hat, ist die symmetrische 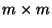 Matrix
Matrix
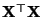 regulär, d.h., es gilt
regulär, d.h., es gilt
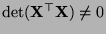 .
.
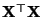 auch invertierbar, d.h., es gibt
eine (eindeutig bestimmte)
auch invertierbar, d.h., es gibt
eine (eindeutig bestimmte) 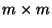 Matrix
Matrix
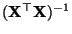 , so dass
wobei
, so dass
wobei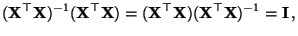
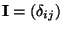 die
die 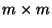 -dimensionale Einheitsmatrix bezeichnet mit
-dimensionale Einheitsmatrix bezeichnet mit
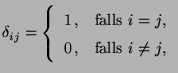
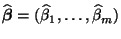 für
den Parametervektor
für
den Parametervektor
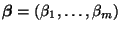 ist ein
sogenannter linearer Schätzer, d.h.,
ist ein
sogenannter linearer Schätzer, d.h.,
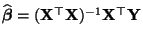 ist eine
lineare Funktion der Zufallsstichprobe
ist eine
lineare Funktion der Zufallsstichprobe
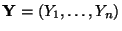 .
.
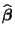 hat die folgenden Güteeigenschaften:
hat die folgenden Güteeigenschaften:
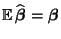 für jedes
für jedes
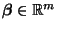 , d.h.,
, d.h.,
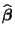 ist erwartungstreu.
ist erwartungstreu.
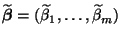 für
für
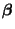 gilt
gilt
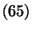 genau dann für jedes
genau dann für jedes
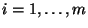 gilt, wenn
gilt, wenn
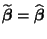 ,
d.h.,
,
d.h.,
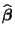 ist bester linearer
erwartungstreuer Schätzer für
ist bester linearer
erwartungstreuer Schätzer für
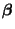 .
.
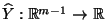 mit
mit
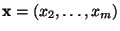 von Werten der
Einflussfaktoren die Zufallsvariable
von Werten der
Einflussfaktoren die Zufallsvariable
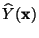 zuordnet,
heißt empirische Regressionshyperebene.
zuordnet,
heißt empirische Regressionshyperebene.
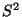 um die empirische
Regressionshyperebene, die gegeben ist durch
um die empirische
Regressionshyperebene, die gegeben ist durch
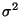 ist, d.h., es gilt
ist, d.h., es gilt
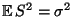 .
.