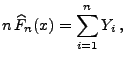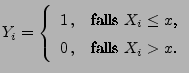Nächste Seite: Satz von Gliwenko-Cantelli
Aufwärts: Empirische Verteilungsfunktion
Vorherige Seite: Empirische Verteilungsfunktion
Inhalt
Definition und elementare
Eigenschaften
- Man kann sich leicht überlegen, dass für jeden Vektor
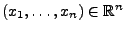 die in (61) definierte
Abbildung
die in (61) definierte
Abbildung
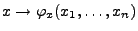 |
(62) |
die Eigenschaften einer Verteilungsfunktion hat.
- Die in (62) gegebene Abbildung wird deshalb
empirische Verteilungsfunktion der (konkreten)
Stichprobe
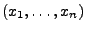 genannt.
genannt.
Dies führt zu der folgenden Begriffsbildung.
- Definition
 Die Abbildung
Die Abbildung
![$ \,\widehat F_n:\mathbb{R}\times\Omega\to[0,1]$](img478.png) mit
mit
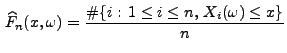 |
(63) |
heißt empirische Verteilungsfunktion der Zufallsstichprobe
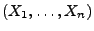 .
.
- Beachte
-
- Die in (63) gegebene Abbildung
kann man als eine Familie
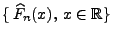 von
Zufallvariablen
von
Zufallvariablen
![$ \,\widehat F_n(x):\Omega\to[0,1]$](img481.png) auffassen.
auffassen.
- Eine solche Familie von Zufallsvariablen wird empirischer Prozess
genannt. Empirische Prozesse bilden eine spezielle Klasse
stochastischer Prozesse, d.h., eine Familie von
Zufallsvariablen, die über einunddemselben
Wahrscheinlichkeitsraum definiert sind.
Theorem 1.17
Für jedes
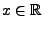
gilt:
- 1.
- Die Zufallsvariable
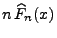 ist binomialverteilt
mit den Parametern
ist binomialverteilt
mit den Parametern 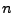 und
und 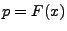 , d.h., es gilt
, d.h., es gilt
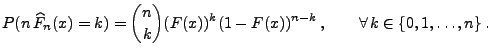 |
(64) |
- 2.
- Insbesondere gilt
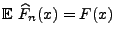 und und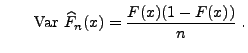 |
(65) |
- 3.
- Mit Wahrscheinlichkeit
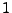 gilt
gilt
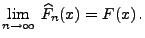 |
(66) |
- 4.
- Falls
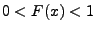 , dann gilt außerdem für jedes
, dann gilt außerdem für jedes
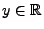
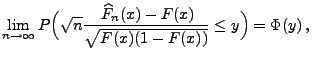 |
(67) |
wobei 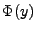 die Verteilungsfunktion der
Standardnormalverteilung ist.
die Verteilungsfunktion der
Standardnormalverteilung ist.
- Beweis
-
- Beachte
 Weil die Zufallsvariable
Weil die Zufallsvariable
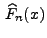 den Erwartungswert
den Erwartungswert
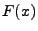 hat (vgl. (65)), kann
hat (vgl. (65)), kann
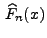 als ein geeigneter Schätzer von
als ein geeigneter Schätzer von 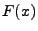 angesehen werden.
angesehen werden.




Nächste Seite: Satz von Gliwenko-Cantelli
Aufwärts: Empirische Verteilungsfunktion
Vorherige Seite: Empirische Verteilungsfunktion
Inhalt
Ursa Pantle
2004-07-14