



Nächste Seite: Diskrete Stichprobenvariablen
Aufwärts: Stichproben und Stichprobenfunktionen
Vorherige Seite: t-Verteilung
Inhalt
Ordnungsstatistiken
- Außer dem Stichprobenmittel
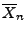 und der
Stichprobenvarianz
und der
Stichprobenvarianz 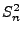 , deren Eigenschaften in den
Abschnitten 1.2 bzw. 1.3 diskutiert
wurden, gibt es noch weitere Stichprobenfunktionen, die bei der
statistischen Datenanalyse von Interesse sind.
, deren Eigenschaften in den
Abschnitten 1.2 bzw. 1.3 diskutiert
wurden, gibt es noch weitere Stichprobenfunktionen, die bei der
statistischen Datenanalyse von Interesse sind.
- Eine solche Klasse von Stichprobenfunktionen sind die sogenannten
Ordnungsstatistiken, die mit Hilfe der folgenden Borel-messbaren
Abbildung
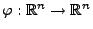 definiert werden:
definiert werden:
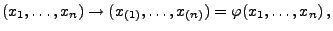 |
(46) |
wobei für jedes
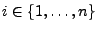
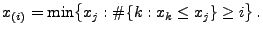 |
(47) |
- Beachte
 Die in (46) und
(47) gegebene Abbildung
Die in (46) und
(47) gegebene Abbildung
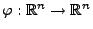 ist eine Borel-messbare Permutation der Komponenten des
Vektors
ist eine Borel-messbare Permutation der Komponenten des
Vektors
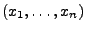 , so dass
, so dass
- Definition
-
- Sei
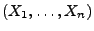 eine beliebige Zufallsstichprobe, und
eine beliebige Zufallsstichprobe, und
- für jedes
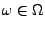 sei
die in (46) und (47) gegebene
(messbare) Permutation von
sei
die in (46) und (47) gegebene
(messbare) Permutation von
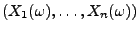 ,
so dass
,
so dass
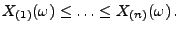 |
(48) |
- Die auf diese Weise definierten Zufallsvariablen
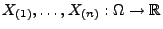 heißen die
Ordnungsstatistiken von
heißen die
Ordnungsstatistiken von
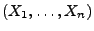 .
.
- Beachte
-
Unterabschnitte




Nächste Seite: Diskrete Stichprobenvariablen
Aufwärts: Stichproben und Stichprobenfunktionen
Vorherige Seite: t-Verteilung
Inhalt
Ursa Pantle
2004-07-14