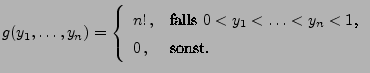Theorem 1.19
Für jede stetige Verteilungsfunktion
![$ F:\mathbb{R}\to[0,1]$](img397.png)
gilt
![$\displaystyle D_n\stackrel{{\rm d}}{=}\sup\limits_{y\in[0,1]}\bigl\vert\,\,\widehat
G_n(y)-y\bigr\vert\,,$](img556.png) |
(78) |
wobei
![$ \,\widehat G_n:\mathbb{R}\times\Omega\to[0,1]$](img557.png)
die empirische
Verteilungsfunktion einer beliebigen Zufallsstichprobe
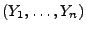
ist, die aus
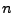
unabhängigen und in dem
Intervall
![$ [0,1]$](img559.png)
gleichverteilten Stichprobenvariablen
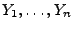
besteht.
Korollar 1.3
Für jede stetige Verteilungsfunktion
![$ F:\mathbb{R}\to[0,1]$](img397.png)
gilt
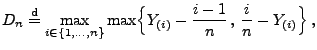 |
(81) |
wobei
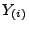
die
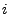
-te Ordnungsstatistik der in
![$ [0,1]$](img559.png)
gleichverteilten Stichprobenvariablen
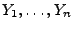
ist.
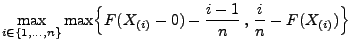
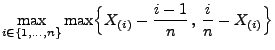
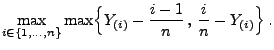
![$\displaystyle P\Bigl(D_n\le\frac{1}{2n}+x\Bigr)=\left\{\begin{array}{ll} 0\,,
...
...\\ [3\jot]
1\,, & \mbox{falls $x\ge\frac{2n-1}{2n}$,}
\end{array}
\right.
$](img583.png)