Nächste Seite: Zwei-Stichproben-Probleme
Aufwärts: Konfidenzintervalle bei Normalverteilung
Vorherige Seite: Konfidenzintervalle für den Erwartungswert
Inhalt
Konfidenzintervalle für die Varianz
In diesem Abschnitt diskutieren wir Konfidenzintervalle für die
Varianz 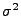 , wobei wir zunächst annehmen, dass der
Erwartungswert
, wobei wir zunächst annehmen, dass der
Erwartungswert 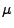 unbekannt ist.
unbekannt ist.
- Aus Theorem 1.11 ergibt sich dann, dass für
beliebige
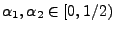 mit
mit
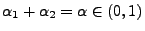
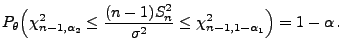 |
(20) |
- Dies ergibt das Konfidenzintervall
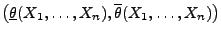 für
für 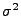 zum Niveau
zum Niveau
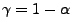 mit
mit
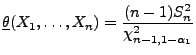 bzw. bzw.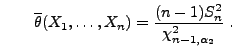 |
(21) |
- Für die Länge
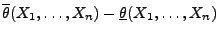 dieses Konfidenzintervalls gilt
dieses Konfidenzintervalls gilt
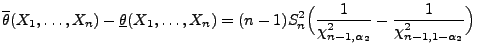 |
(22) |
mit
Falls der Erwartungswert 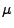 bekannt ist, dann lässt sich mit
Hilfe der modifizierten Stichprobenvarianz
bekannt ist, dann lässt sich mit
Hilfe der modifizierten Stichprobenvarianz
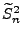 ein
weiteres Konfidenzintervall für die Varianz
ein
weiteres Konfidenzintervall für die Varianz 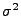 konstruieren, wobei
konstruieren, wobei
- Beachte
-
- Die in (25) gegebene Länge
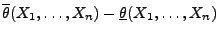 des modifizierten Konfidenzintervalls kann größer als die
Länge (22) des Intervalls sein, das in
(21) für den Fall betrachtet wurde, dass der
Ertwartungswert
des modifizierten Konfidenzintervalls kann größer als die
Länge (22) des Intervalls sein, das in
(21) für den Fall betrachtet wurde, dass der
Ertwartungswert 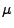 unbekannt ist.
unbekannt ist.
- Der Grund hierfür ist, dass ,,untypische'' Stichprobenwerte, die
große Abweichungen vom Erwartungswert
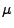 aufweisen, besser
durch das Stichprobenmittel
aufweisen, besser
durch das Stichprobenmittel
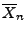 als durch
als durch 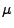 kompensiert werden.
kompensiert werden.




Nächste Seite: Zwei-Stichproben-Probleme
Aufwärts: Konfidenzintervalle bei Normalverteilung
Vorherige Seite: Konfidenzintervalle für den Erwartungswert
Inhalt
Ursa Pantle
2004-07-14
![]() bekannt ist, dann lässt sich mit
Hilfe der modifizierten Stichprobenvarianz
bekannt ist, dann lässt sich mit
Hilfe der modifizierten Stichprobenvarianz
![]() ein
weiteres Konfidenzintervall für die Varianz
ein
weiteres Konfidenzintervall für die Varianz ![]() konstruieren, wobei
konstruieren, wobei