



Nächste Seite: Null-Hypothese und Alternativ-Hypothese; kritischer
Aufwärts: Tests statistischer Hypothesen
Vorherige Seite: Tests statistischer Hypothesen
Inhalt
Problemstellung und
Modellbeschreibung
Genauso wie in Kapitel 1-3 nehmen
wir auch in diesem Kapitel an, dass
- die Stichprobenvariablen
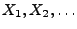 unabhängig und
identisch verteilt sind und dass
unabhängig und
identisch verteilt sind und dass
- der Wahrscheinlichkeitsraum
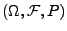 , über dem die
Stichprobenvariablen
, über dem die
Stichprobenvariablen
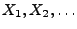 definiert sind, der
kanonische Wahrscheinlichkeitsraum dieser Zufallsvariablen
ist.
definiert sind, der
kanonische Wahrscheinlichkeitsraum dieser Zufallsvariablen
ist.
- Dabei prüfen wir nun Hypothesen (d.h. Vermutungen) über die
Beschaffenheit der unbekannten Verteilung bzw. der
Verteilungsfunktion der Stichprobenvariablen
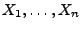 .
.
In dieser einführenden Vorlesung untersuchen wir vor allem
- parametrische Tests, bei denen vorausgesetzt wird, dass
die Verteilung der Stichprobenvariablen
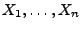 zu
einer vorgegebenen parametrischen Familie von
Verteilungen
zu
einer vorgegebenen parametrischen Familie von
Verteilungen
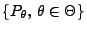 gehört;
gehört;
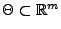 mit
mit 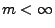 .
.
Darüber hinaus gibt es aber auch
- nichtparametrische Tests, bei denen nicht
vorausgesetzt wird, dass
die Verteilung der Stichprobenvariablen
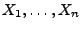 zu
einer vorgegebenen parametrischen Familie von
Verteilungen gehört, vgl. die Vorlesung ,,Statistik II''.
zu
einer vorgegebenen parametrischen Familie von
Verteilungen gehört, vgl. die Vorlesung ,,Statistik II''.
- Beachte
-
- Wir betrachten zunächst lediglich sogenannte
nichtrandomisierte Tests.
- Die Entscheidung, ob eine Hypothese verworfen wird (bzw. ob sie
nicht verworfen wird), hängt dabei nur von den beobachten Daten
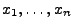 ab, d.h. von der beobachteten Realisierung
ab, d.h. von der beobachteten Realisierung
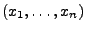 der Zufallsstichprobe
der Zufallsstichprobe
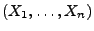 .
.
- Die Entscheidungsregel wird so konstruiert, dass die
Wahrscheinlichkeiten von Fehlentscheidungen möglichst klein sind
(bzw. vorgegebene Schwellenwerte nicht überschreiten).
- Dabei kann man ähnlich wie bei der Konstruktion von
Konfidenzintervallen zu einem (vorgegebenen) Konfidenzniveau
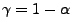 vorgehen, die in Abschnitt 3
diskutiert worden sind,
vorgehen, die in Abschnitt 3
diskutiert worden sind,
- denn bei einem Konfidenzintervall
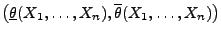 für einen unbekannten Parameterwert
für einen unbekannten Parameterwert 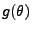 kann man
kann man 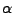 als die ,,Fehlerwahrscheinlichkeit'' interpretieren, dass der Wert
als die ,,Fehlerwahrscheinlichkeit'' interpretieren, dass der Wert
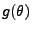 nicht von dem Konfidenzintervall
nicht von dem Konfidenzintervall
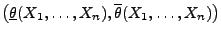 überdeckt wird, d.h., dass
überdeckt wird, d.h., dass 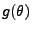 nicht innerhalb der
Schranken
nicht innerhalb der
Schranken
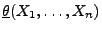 bzw.
bzw.
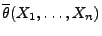 liegt.
liegt.
Unterabschnitte




Nächste Seite: Null-Hypothese und Alternativ-Hypothese; kritischer
Aufwärts: Tests statistischer Hypothesen
Vorherige Seite: Tests statistischer Hypothesen
Inhalt
Ursa Pantle
2004-07-14