



Nächste Seite: Fehlerwahrscheinlichkeiten
Aufwärts: Problemstellung und Modellbeschreibung
Vorherige Seite: Problemstellung und Modellbeschreibung
Inhalt
Null-Hypothese und Alternativ-Hypothese; kritischer
Bereich
Sei 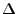 die Familie der insgesamt in Betracht gezogenen (d.h.
potentiell möglichen bzw. zulässigen) Verteilungsfunktionen
die Familie der insgesamt in Betracht gezogenen (d.h.
potentiell möglichen bzw. zulässigen) Verteilungsfunktionen 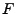 der Stichprobenvariablen
der Stichprobenvariablen
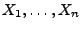 .
Dabei ist die folgende Sprechweise üblich:
.
Dabei ist die folgende Sprechweise üblich:
- Die Hypothese
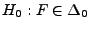 heißt Nullhypothese,
während
heißt Nullhypothese,
während
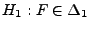 Alternativhypothese genannt
wird.
Alternativhypothese genannt
wird.
- Die Nullhypothese
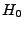 bzw. die Alternativhypothese
bzw. die Alternativhypothese 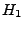 heißen
einfach, falls die Teilmenge
heißen
einfach, falls die Teilmenge 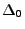 bzw.
bzw. 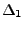 nur
aus einem Element besteht. Ansonsten sagt man, dass
nur
aus einem Element besteht. Ansonsten sagt man, dass 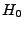 bzw.
bzw.
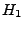 zusammengesetzte Hypothesen sind.
zusammengesetzte Hypothesen sind.
Um zwischen der Nullhypothese 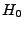 und der Alternativhypothese
und der Alternativhypothese
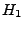 abwägen zu können, wird ein Test, d.h. eine
Entscheidungsregel nach dem folgenden Prinzip konstruiert:
abwägen zu können, wird ein Test, d.h. eine
Entscheidungsregel nach dem folgenden Prinzip konstruiert:
- Der Stichprobenraum
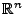 wird in zwei Borel-Mengen
wird in zwei Borel-Mengen 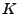 und
und
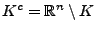 zerlegt.
zerlegt.
- Dabei heißt
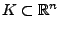 der kritische Bereich (d.h. der
Ablehnungsbereich der Nullhypothese
der kritische Bereich (d.h. der
Ablehnungsbereich der Nullhypothese 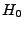 ).
).
- Die Nullhypothese
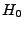 wird verworfen (d.h. abgelehnt), falls
wird verworfen (d.h. abgelehnt), falls
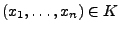 .
.
- Ansonsten, d.h., falls
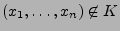 , wird
, wird 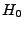 nicht verworfen.
nicht verworfen.
Mit anderen Worten:
Dies führt zu der folgenden
- Definition
 Sei
Sei
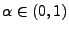 eine beliebige, jedoch
vorgegebene Zahl. Man sagt, dass die in (1)
eingeführte Stichprobenfunktion
eine beliebige, jedoch
vorgegebene Zahl. Man sagt, dass die in (1)
eingeführte Stichprobenfunktion
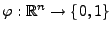 ein
ein




Nächste Seite: Fehlerwahrscheinlichkeiten
Aufwärts: Problemstellung und Modellbeschreibung
Vorherige Seite: Problemstellung und Modellbeschreibung
Inhalt
Ursa Pantle
2004-07-14