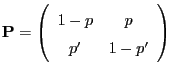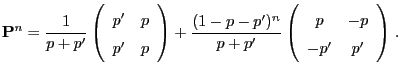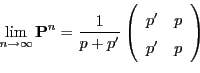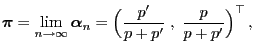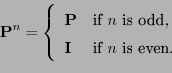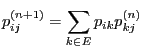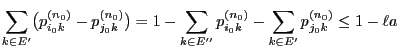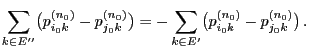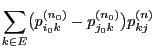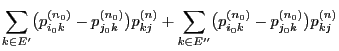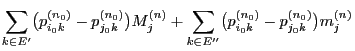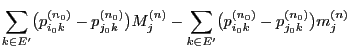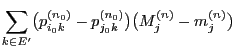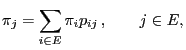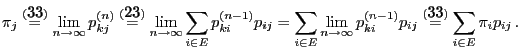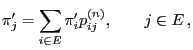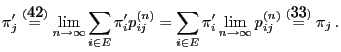Next: Estimates for the Rate
Up: Ergodicity and Stationarity
Previous: Ergodicity and Stationarity
Contents
Basic Definitions and Quasi-positive
Transition Matrices
This serves as a motivation to formally introduce the notion of the
ergodicity of Markov chains.
- Definition
 The Markov chain
The Markov chain
 with
transition matrix
with
transition matrix
 and the corresponding
and the corresponding  -step
transition matrices
-step
transition matrices
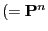 ) is
called ergodic if the limits
) is
called ergodic if the limits
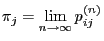 |
(33) |
- exist for all
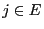
- are positive and independent of
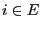
- form a probability function
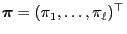 ,
i.e.
,
i.e.
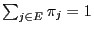 .
.
- Example
 (Weather Forecast)
(Weather Forecast)
- In order to illustrate the notion of an ergodic Markov chain we
return to the simple example of weather forecast already discussed
in Sections 2.1.2 and 2.1.4.
- Let
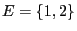 and
an arbitrary transition matrix such that
and
an arbitrary transition matrix such that
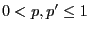 .
.
- The
 -step transition matrix
-step transition matrix
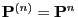 is given by
is given by
- If
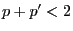 , this and (26) imply
and
, this and (26) imply
and
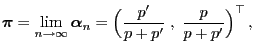 |
(34) |
respectively. Note that the limit distribution
 in
(34) does not depend on the choice of the
initial distribution
in
(34) does not depend on the choice of the
initial distribution
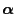
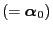 .
.
- However, if
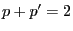 , then
, then
The ergodicity of Markov chains on an arbitrary finite state space
can be characterized by the following notion from the theory of
positive matrices.
- Definition
-
- The
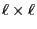 matrix
matrix
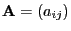 is called non-negative if all entries
is called non-negative if all entries 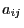 of
of
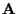 are non-negative.
are non-negative.
- The non-negative matrix
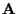 is called quasi-positive if
there is a natural number
is called quasi-positive if
there is a natural number 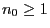 such that all entries of
such that all entries of
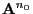 are positive.
are positive.
- Remark
-
If
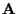 is a stochastic matrix and we can find a natural number
is a stochastic matrix and we can find a natural number
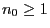 such that all entries of
such that all entries of
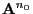 are positive,
then it is easy to see that for all natural numbers
are positive,
then it is easy to see that for all natural numbers 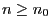 all
entries of
all
entries of
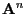 are positive.
are positive.
Theorem 2.4
The Markov chain
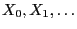
with state space
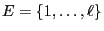
and transition matrix

is ergodic if
and only if

is quasi-positive.
- Proof
-
- Remarks
-
- As the limits
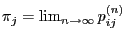 of ergodic
Markov chains do not depend on
of ergodic
Markov chains do not depend on 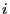 and the state space
and the state space
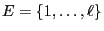 is finite, clearly
is finite, clearly
- The proof of Theorem 2.4 does not only show the
existence of the limits
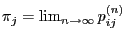 but
also yields the following estimate for the rate of
convergence: The inequality (37) implies
but
also yields the following estimate for the rate of
convergence: The inequality (37) implies
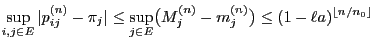 |
(39) |
and hence
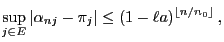 |
(40) |
where
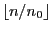 denotes the integer part of
denotes the integer part of
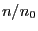 .
.
- Estimates like (39) and (40) are
referred to as geometric bounds for the rate of convergence in
literature.
Now we will show that the limits
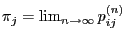 can be regarded as solution of a system of linear
equations.
can be regarded as solution of a system of linear
equations.
- Proof
-
- The definition (33) of the limits
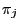 and the
Chapman-Kolmogorov equation (23) imply by changing
the order of limit and sum that
and the
Chapman-Kolmogorov equation (23) imply by changing
the order of limit and sum that
- Suppose now that there is another solution
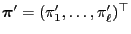 of
(41) such that
of
(41) such that
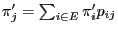 for all
for all 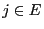 and
and
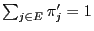 .
.
- By induction one easily shows
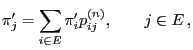 |
(42) |
for all
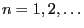 .
.
- In particular (42) implies

- Remarks
-
- In matrix notation the linear equation system (41) is
of the form
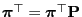 .
.
- If the number
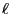 of elements in the state space is reasonably
small this equation system can be used for the numerical
calculation of the probability function
of elements in the state space is reasonably
small this equation system can be used for the numerical
calculation of the probability function
 ; see
Section 2.2.5.
; see
Section 2.2.5.
- In case
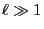 , Monte-Carlo simulation turns out to be a
more efficient method to determine
, Monte-Carlo simulation turns out to be a
more efficient method to determine
 ; see
Section 3.3.
; see
Section 3.3.




Next: Estimates for the Rate
Up: Ergodicity and Stationarity
Previous: Ergodicity and Stationarity
Contents
Ursa Pantle
2006-07-20
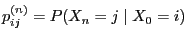 of
the random state
of
the random state 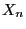
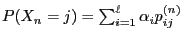 of
of 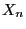
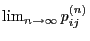 and
and
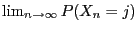 , respectively, as well
as their equality and independence of
, respectively, as well
as their equality and independence of 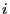 ,
,
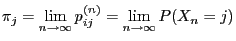 as approximation of
as approximation of
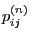 and
and 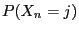 if
if 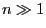 .
.