



Next: Dirichlet-Forms and Rayleigh-Theorem
Up: Reversibility; Estimates for the
Previous: Multiplicative Reversible Version of
Contents
Alternative Estimate for the Rate of Convergence;
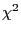 Contrast
Contrast
Based on the multiplicative reversible version
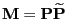 of the ergodic (but not necessarily
reversible) transition matrix
of the ergodic (but not necessarily
reversible) transition matrix
 we will now deduce an
alternative estimate for the rate of convergence
we will now deduce an
alternative estimate for the rate of convergence
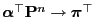 for
for
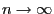 ; see
Theorem 2.16.
; see
Theorem 2.16.
The following abbreviations and lemmata will turn out to be useful
in the proof of Theorem 2.16.
- Proof
-
- Introducing the notation
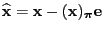 we obtain that
we obtain that
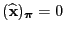 and
where the last but one equality follows from the definition
(99) of the matrix
and
where the last but one equality follows from the definition
(99) of the matrix
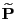 .
.
- This implies
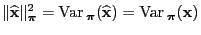 and and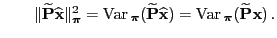 |
(107) |
- On the other hand
and thus
as
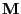 is a stochastic matrix such that
is a stochastic matrix such that
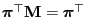 and therefore
and therefore
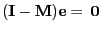 and
and
- Taking into account (107) this shows the validity of
(106).

We introduce the following notions.
The distance
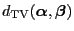 between
between
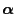 and
and
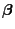 can be estimated via the
can be estimated via the 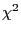 -contrast
-contrast
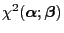 of
of
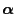 with respect to
with respect to
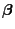 as follows.
as follows.
- Proof
-
- Taking into account that
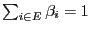 , an application
of the Cauchy-Schwarz inequality yields
, an application
of the Cauchy-Schwarz inequality yields
- This implies the assertion of the lemma.

The rate of convergence
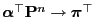 for
for
 can now be estimated based on
can now be estimated based on
- the second largest eigenvalue
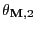 of the
multiplicative reversible version
of the
multiplicative reversible version
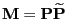 of
the (ergodic) transition matrix
of
the (ergodic) transition matrix

- and the
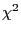 contrast
contrast
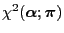 of the initial
distribution
of the initial
distribution
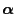 with respect to the stationary limit
distribution
with respect to the stationary limit
distribution
 .
.
Theorem 2.16

For any initial distribution
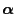
and for all
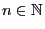
,
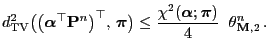 |
(112) |
- Proof
-
- Let
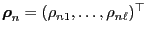 where
where
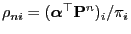 .
.
- Then for all
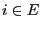 and thus
and thus
- Moreover, by definition (110) of the
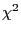 contrast
contrast
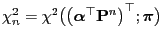 of
of
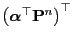 with respect to
with respect to
 we obtain
we obtain
i.e.,
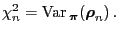 |
(113) |
- Now the identity (106) derived in
Lemma 2.6 yields
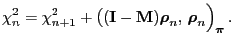 |
(114) |
- On the other hand the spectral representation (101)
of
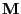 derived in Theorem 2.15 implies
derived in Theorem 2.15 implies
as
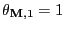 ,
,
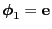 and
and
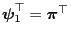 and therefore
and therefore
- Summarizing our results we have seen that




Next: Dirichlet-Forms and Rayleigh-Theorem
Up: Reversibility; Estimates for the
Previous: Multiplicative Reversible Version of
Contents
Ursa Pantle
2006-07-20
![]() of the ergodic (but not necessarily
reversible) transition matrix
of the ergodic (but not necessarily
reversible) transition matrix
![]() we will now deduce an
alternative estimate for the rate of convergence
we will now deduce an
alternative estimate for the rate of convergence
![]() for
for
![]() ; see
Theorem 2.16.
; see
Theorem 2.16.
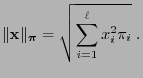
![]() between
between
![]() and
and
![]() can be estimated via the
can be estimated via the ![]() -contrast
-contrast
![]() of
of
![]() with respect to
with respect to
![]() as follows.
as follows.
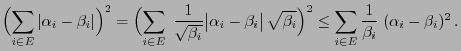
![]() for
for
![]() can now be estimated based on
can now be estimated based on