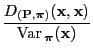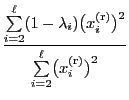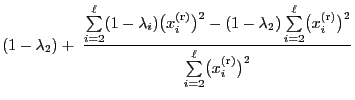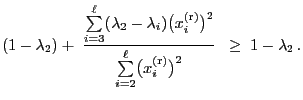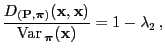Next: Bounds for the Eigenvalues
Up: Reversibility; Estimates for the
Previous: Alternative Estimate for the
Contents
Dirichlet-Forms and Rayleigh-Theorem
- Let
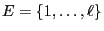 be an arbitrary finite set and let
be an arbitrary finite set and let
 be an
be an
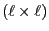 -dimensional transition matrix,
which is irreducible and aperiodic (i.e. quasi-positive) as well
as reversible.
-dimensional transition matrix,
which is irreducible and aperiodic (i.e. quasi-positive) as well
as reversible.
- Recall that
- all eigenvalues of
 are real (see
Section 2.3.3), and
are real (see
Section 2.3.3), and
- by the Perron-Frobenius theorem (see Theorem 2.6
and Corollary 2.3) the eigenvalues of
 are in
the interval
are in
the interval ![$ (-1,1]$](img901.png) , where
, where
- the largest eigenvalue is
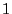 and the absolute values of the other
eigenvalues are (strictly) less than
and the absolute values of the other
eigenvalues are (strictly) less than 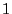 .
.
- Remarks
-
In order to derive an upper bound for 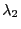 , we need a
representation formula for
, we need a
representation formula for 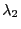 ,
,
First of all we will show the following lemma.
- Proof
 From the definition (103) of the inner product and the
reversibility of the pair
From the definition (103) of the inner product and the
reversibility of the pair
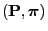 we obtain
we obtain

We will now prove the Rayleigh-theorem that yields a
representation formula for the second largest eigenvalue
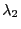 of the reversible pair
of the reversible pair
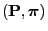 .
.
- Proof
-
- Lemma 2.8 implies for arbitrary
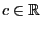 and
and
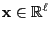
- On the other hand as
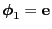 and the eigenvectors
and the eigenvectors
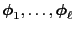 are orthonormal with respect to the inner product
are orthonormal with respect to the inner product
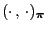 we can conclude that
we can conclude that




Next: Bounds for the Eigenvalues
Up: Reversibility; Estimates for the
Previous: Alternative Estimate for the
Contents
Ursa Pantle
2006-07-20
![]() , we need a
representation formula for
, we need a
representation formula for ![]() ,
,
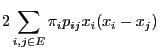
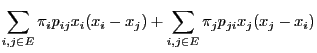
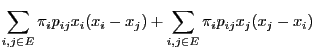
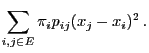
![]() of the reversible pair
of the reversible pair
![]() .
.
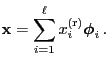
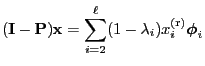 and hence
and hence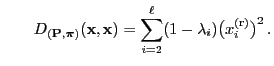
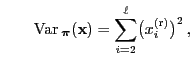 if
if