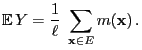Next: Gibbs Sampler
Up: Simulation Methods Based on
Previous: Simulation Methods Based on
Contents
Example: Hard-Core Model
(see O. Häggström (2002) Finite Markov Chains and Algorithmic
Applications. CU Press, Cambridge)
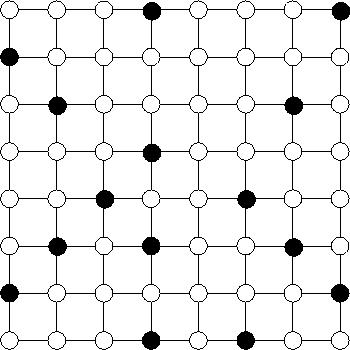
Figure 6:
Lattice 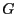 of size
of size 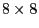 , black pixels are
corresponding to value
, black pixels are
corresponding to value 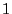
|
|
- If the numbers
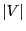 and
and 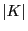 of vertices and edges,
respectively, of the connected graph
of vertices and edges,
respectively, of the connected graph 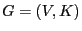 are large,
are large,
- the explicit description of the admissible configurations
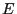 will
cause difficulties.
will
cause difficulties.
- Therefore, the number
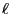 of all admissible configurations is
typically unknown.
of all admissible configurations is
typically unknown.
- Consequently, formula (30) cannot be applied
directly for the simulation of ,,randomly'' picked admissible
configurations.
- MCMC Simulation Algorithm
-
- Alternatively, a Markov chain
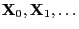 can be
constructed
can be
constructed
- that has the state space
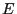 and an (appropriately chosen)
irreducible and aperiodic transition matrix
and an (appropriately chosen)
irreducible and aperiodic transition matrix
 ,
,
- such that the ergodic limit distribution
 is given by
(30).
is given by
(30).
- Then we generate a path
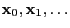 of the Markov
chain using the recursive construction of Markov chains that has
been discussed in Section 2.1.3:
of the Markov
chain using the recursive construction of Markov chains that has
been discussed in Section 2.1.3:
- Pick an admissible initial configuration
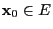 .
.
- Pick an arbitrary vertex
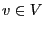 ,,at random'' and toss a fair
coin.
,,at random'' and toss a fair
coin.
- If the event ,,head'' occurs and if
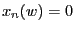 for all vertices
for all vertices
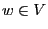 connected to
connected to 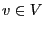 , then set
, then set
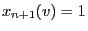 ; else set
; else set
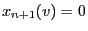 .
.
- The values of all edges
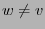 are not changed, i.e.,
are not changed, i.e.,
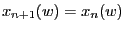 for all
for all 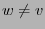 .
.
- Remarks
-
- In order to implement steps 2 - 4 of this algorithm, the update
function
![$ \varphi:E\times[0,1]\to E$](img753.png) considered in
(2.19) needs to be specified.
considered in
(2.19) needs to be specified.
- For this purpose the unit interval
![$ (0,1]$](img165.png) is divided into
is divided into 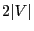 parts of equal length
parts of equal length 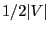
- The following theorem implies that for sufficiently large
 the
return
the
return
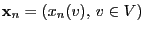 of the algorithm can be
regarded as a configuration that has been approximately picked
according to the distribution
of the algorithm can be
regarded as a configuration that has been approximately picked
according to the distribution
 .
.
Theorem 3.10
- Let
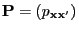 be the transition matrix of
the MCMC algorithm simulating the hard core model in
be the transition matrix of
the MCMC algorithm simulating the hard core model in
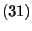 and let
and let
 be the probability function
given in
be the probability function
given in
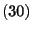 .
.
- Then
 is irreducible and aperiodic and the pair
is irreducible and aperiodic and the pair
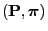 is reversible.
is reversible.
- Proof
-
- Remarks
-




Next: Gibbs Sampler
Up: Simulation Methods Based on
Previous: Simulation Methods Based on
Contents
Ursa Pantle
2006-07-20
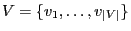
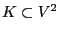 of edges, each of them connecting
two vertices.
of edges, each of them connecting
two vertices.
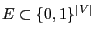 of
admissible configurations,
of
admissible configurations,
 on both vertices; see also
Figure 6.
on both vertices; see also
Figure 6.
![$\displaystyle x^\prime(v_i)=\left\{\begin{array}{ll} 1&\mbox{if $\displaystyle ...
...c{2i-2}{2\vert V\vert}\;,\;\frac{2i}{2\vert V\vert}\Bigr]$.} \end{array}\right.$](img1537.png)