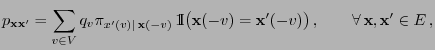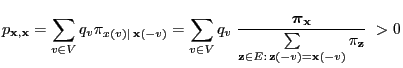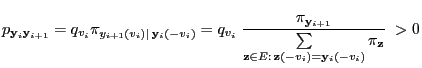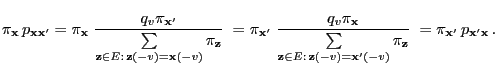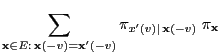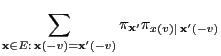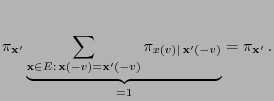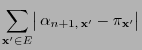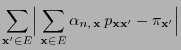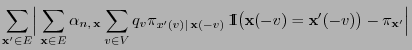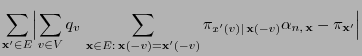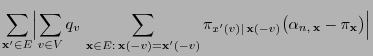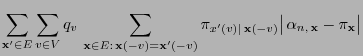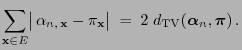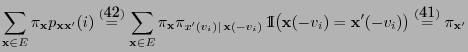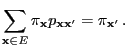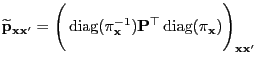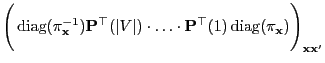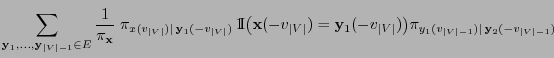Next: Metropolis-Hastings Algorithm
Up: Simulation Methods Based on
Previous: Example: Hard-Core Model
Contents
Gibbs Sampler
The MCMC algorithm for the generation of ,,randomly picked''
admissible configurations of the hard core model (see
Section 3.3.1) is a special case of a so-called Gibbs sampler for the simulation of discrete (high dimensional)
random vectors.
- MCMC Simulation Algorithm
-
Theorem 3.11

Let the transition matrix
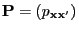
be given
as
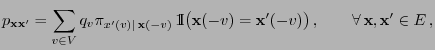 |
(36) |
where the conditional probabilities
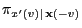
are defined in
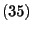
. Then

is
irreducible and aperiodic and the pair
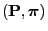
is
reversible.
- Proof
 The assertion can be proved similarly to the proof of
Theorem 3.10.
The assertion can be proved similarly to the proof of
Theorem 3.10.
- In order to see that
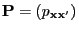 is aperiodic it
suffices to notice
is aperiodic it
suffices to notice
- that for all
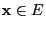
- and hence all diagonal elements
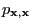 of
of
 are
positive.
are
positive.
- The following considerations show that
 is irreducible.
is irreducible.
- It is left to show that the detailed balance equation
(2.85) holds, i.e.
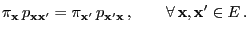 |
(38) |
Let
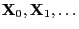 be a Markov chain with state space
be a Markov chain with state space
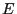 and the transition matrix
and the transition matrix
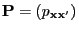 given by (36). As a consequence of
Theorem 3.11 we get that in this case
given by (36). As a consequence of
Theorem 3.11 we get that in this case
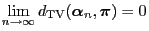 |
(39) |
for any initial concentration
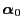 where
where
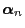 denotes the distribution of
denotes the distribution of
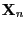 . Furthermore, the Gibbs
sampler shows the following monotonic behavior.
. Furthermore, the Gibbs
sampler shows the following monotonic behavior.
- Proof
-
- Remarks
-
Theorem 3.13

The matrix
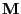
has the following
representation
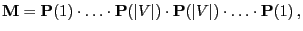 |
(45) |
i.e., the multiplicative reversible version
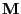
of the
,,forward-scan matrix''

coincides with the
,,forward-backward scan matrix''.
- Proof
-
- Remarks
-
- If Gibbs samplers are used in practice it is always assumed
- The family
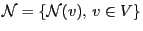 of subsets of
of subsets of 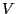 is called
a system of neighborhoods if for arbitrary
is called
a system of neighborhoods if for arbitrary 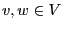
- (a)
-
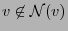 ,
,
- (b)
-
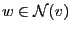 implies
implies
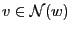 .
.
- For the hard-core model from Section 3.3.1,
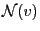 is the set of those vertices
is the set of those vertices 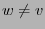 that are
directly connected to
that are
directly connected to 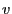 by an edge.
by an edge.




Next: Metropolis-Hastings Algorithm
Up: Simulation Methods Based on
Previous: Example: Hard-Core Model
Contents
Ursa Pantle
2006-07-20
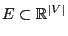 with
probability
with
probability 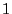 where we assume
where we assume
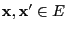 there is a finite
sequence of states
there is a finite
sequence of states
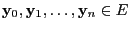 such that
such that
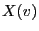 of
of
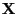 has the value
has the value 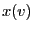
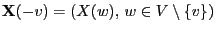 of
the other components equals
of
the other components equals
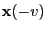 where we assume
where we assume
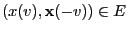 .
.