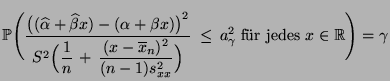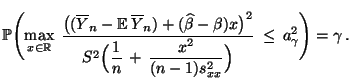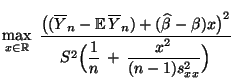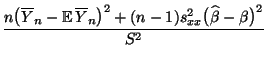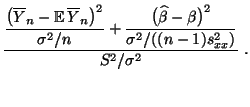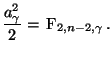Next: Einfaktorielle Varianzanalyse
Up: Einfache lineare Regression
Previous: Konfidenzintervalle; Prognose von Zielwerten
Contents
Simultane
Konfidenzbereiche; Konfidenzbänder
- Auf ähnliche Weise wie in Theorem 2.6 kann man
sogenannte simultane Konfidenzbereiche zum Niveau
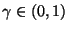 gleichzeitig für meherere erwartete Zielwerte
gleichzeitig für meherere erwartete Zielwerte
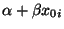 ,
,
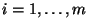 herleiten, die vorgegebenen (Ausgangs-)
Werten
herleiten, die vorgegebenen (Ausgangs-)
Werten
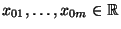 entsprechen.
entsprechen.
- Dabei ist erneut der Fall
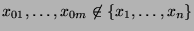 von besonderem
Interesse, d.h., wenn an den Stellen
von besonderem
Interesse, d.h., wenn an den Stellen
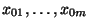 keine
Daten erhoben werden.
keine
Daten erhoben werden.
Hierfür ist die folgende Bonferroni-Ungleichung nützlich,
vgl. auch Übungsaufgabe WR-1.5.
Lemma 2.4

Für jede natürliche Zahl
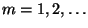
und für beliebige
Ereignisse
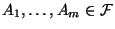
gilt
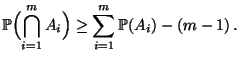 |
(46) |
- Beweis
 Aus der Subadditivität von Wahrscheinlichkeitsmaßen (vgl.
Theorem WR-2.2) ergibt sich, daß
Aus der Subadditivität von Wahrscheinlichkeitsmaßen (vgl.
Theorem WR-2.2) ergibt sich, daß

Theorem 2.8

Die Wahrscheinlichkeit, daß
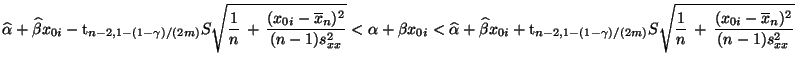 |
(47) |
gleichzeitig für jedes
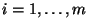
gilt, ist mindestens gleich
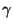
.
- Beweis
-
- Gemäß Teilaussage 2 von Theorem 2.6 ist die
Wahrscheinlichkeit für jedes der
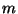 Ereignisse
Ereignisse
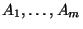 in (47) gegeben durch
in (47) gegeben durch
- Aus Lemma 2.4 ergibt sich nun für die
Wahrscheinlichkeit des Durchschnittes
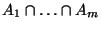 , daß
, daß

- Beachte
-
Bei der Lösung dieser Fragestellung ist die Klasse der
F-Verteilungen nützlich, vgl. Abschnitt I.3.1.3.
Außerdem ist der folgende Hilfssatz nützlich.
Lemma 2.5

Seien
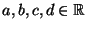
beliebige reelle Zahlen mit
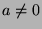
,
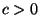
und
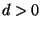
. Dann gilt
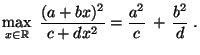 |
(50) |
.
- Beweis
-
- Die Behauptung gilt genau dann, wenn für alle
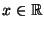 und wenn es ein
und wenn es ein
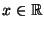 gibt, so daß beide Seiten dieser
Ungleichung übereinstimmen.
gibt, so daß beide Seiten dieser
Ungleichung übereinstimmen.
- Die Ungleichung gilt genau dann, wenn
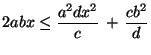
bzw.
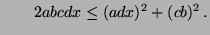
- Die letzte Ungleichung ist offenbar richtig, und für
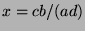 gilt die Gleichheit.
gilt die Gleichheit.

Theorem 2.9

Sei
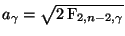
. Dann ist durch
die in
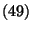
definierte Menge
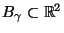
ein Konfidenzband zum Niveau
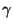
für
die Regressionsgerade
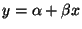
gegeben.
- Beweis
-
- Die Behauptung ist bewiesen, wenn wir zeigen, daß
bzw.
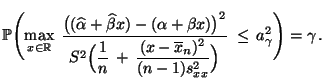 |
(51) |
- Aus (16) ergibt sich, daß
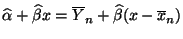 . Weil
. Weil
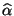 und
und
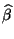 erwartungstreue Schätzer für
erwartungstreue Schätzer für 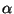 bzw.
bzw. 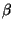 sind, gilt
außerdem, daß
sind, gilt
außerdem, daß
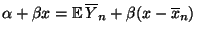 .
.
- Wir führen deshalb die gleiche Skalenverschiebung durch, die wir
bereits im Beweis von Theorem 2.5 betrachtet haben:
d.h. wir nehmen (o.B.d.A.) an, daß
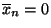 .
.
- Mit anderen Worten: Anstelle (51) zeigen wir, daß es
eine Zahl
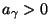 gibt, so daß
gibt, so daß
- Weil
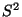 nicht von
nicht von 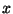 abhängt, ergibt sich aus
Lemma 2.5, daß
abhängt, ergibt sich aus
Lemma 2.5, daß
- Weil
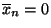 und weil demzufolge
und weil demzufolge
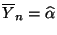 gilt, ergibt sich aus
Theorem 2.5, daß die Zufallsvariablen
gilt, ergibt sich aus
Theorem 2.5, daß die Zufallsvariablen
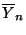 und
und
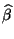 normalverteilt und unkorreliert (und
somit gemäß Teilaussage 2 von Lemma 2.3 auch
unabhängig) sind, vgl. auch Übungsaufgabe 2.3.
normalverteilt und unkorreliert (und
somit gemäß Teilaussage 2 von Lemma 2.3 auch
unabhängig) sind, vgl. auch Übungsaufgabe 2.3.
- Der Zähler des letzten Quotienten ist also die Summe der Quadrate
von zwei unabhängigen N
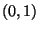 -verteilten Zufallsvariablen, d.h.,
der Zähler ist
-verteilten Zufallsvariablen, d.h.,
der Zähler ist 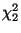 -verteilt.
-verteilt.
- Außerdem ergibt sich aus Theorem 2.5, daß Zähler und
Nenner unabhängig sind und daß
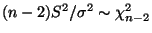 .
.
- Hieraus und aus der Definition der F-Verteilung folgt, daß
(51) gilt, falls

- Beachte
-
- Es gilt t
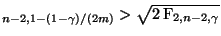 für jedes hinreichend große
für jedes hinreichend große 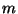 , vgl.
Übungsaufgabe 3.3a.
, vgl.
Übungsaufgabe 3.3a.
- Hieraus folgt, daß der simultane Konfidenzbereich, der in
Theorem 2.8 mit Hilfe der Bonferroni-Ungleichung
(46) hergeleitet worden ist, für große
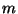 größer ist als der simultane Konfidenzbereich, der sich aus dem
in Theorem 2.9 konstruierten Konfidenzband ergibt.
größer ist als der simultane Konfidenzbereich, der sich aus dem
in Theorem 2.9 konstruierten Konfidenzband ergibt.
- Auf den ersten Blick scheint dies ein Widerspruch zu sein, weil in
Theorem 2.9 die Überdeckungseigenschaft für alle
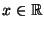 gefordert wird, während diese Eigenschaft in
Theorem 2.8 nur für endlich viele
Ausgangswerte
gefordert wird, während diese Eigenschaft in
Theorem 2.8 nur für endlich viele
Ausgangswerte
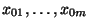 betrachtet wird.
betrachtet wird.
- Der Grund, daß Theorem 2.9 für große
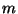 zu
kleineren (d.h. besseren) simultanen Konfidenzbereichen führt,
besteht darin, daß die Bonferroni-Ungleichung (46)
für große
zu
kleineren (d.h. besseren) simultanen Konfidenzbereichen führt,
besteht darin, daß die Bonferroni-Ungleichung (46)
für große 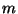 nur eine sehr ungenaue untere Schranke für die
Wahrscheinlichkeit
nur eine sehr ungenaue untere Schranke für die
Wahrscheinlichkeit
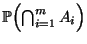 liefert.
liefert.




Next: Einfaktorielle Varianzanalyse
Up: Einfache lineare Regression
Previous: Konfidenzintervalle; Prognose von Zielwerten
Contents
Ursa Pantle
2003-03-10
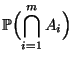
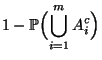
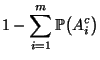
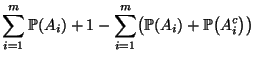
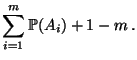
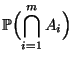
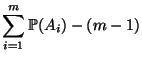
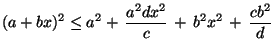
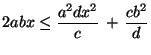 bzw.
bzw.