



Next: Schätzbare Funktionen
Up: Schätzung der Modellparameter
Previous: Schätzung der Modellparameter
Contents
Methode der kleinsten Quadrate; verallgemeinerte Inverse
- Um einen MKQ-Schätzer für den Parametervektor
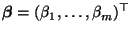 zu konstruieren,
bestimmen wir ähnlich wie in Abschnitt 3.1.2 einen
Vektor
zu konstruieren,
bestimmen wir ähnlich wie in Abschnitt 3.1.2 einen
Vektor
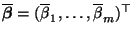 ,
so daß der mittlere quadratische Fehler
,
so daß der mittlere quadratische Fehler
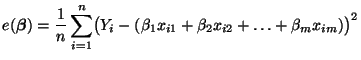 |
(17) |
für
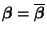 minimal wird.
minimal wird.
- Aus (17) folgt, daß jedes solche Extremum
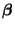 der Vektorgleichung
der Vektorgleichung
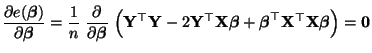 |
(18) |
genügen muß.
- Die Berechnung der partiellen Ableitungen in (18)
ergibt somit, daß jeder Vektor
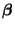 , für den der in
(17) gegebene mittlere quadratische Fehler
, für den der in
(17) gegebene mittlere quadratische Fehler
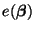 minimal ist, eine Lösung des folgenden
Gleichungssystems sein muß:
minimal ist, eine Lösung des folgenden
Gleichungssystems sein muß:
- Mit anderen Worten: Jedes solche Extremum
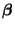 genügt den
sogenannten Normalengleichungen
genügt den
sogenannten Normalengleichungen
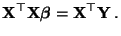 |
(19) |
- Beachte
-
- Weil wir in diesem Abschnitt annehmen, daß die Designmatrix
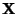 keinen vollen Rang besitzt, ist die
keinen vollen Rang besitzt, ist die 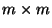 Matrix
Matrix
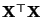 nicht invertierbar, denn es gilt
nicht invertierbar, denn es gilt
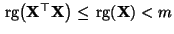 .
.
- Die Normalengleichungen (19) besitzen deshalb keine
eindeutig bestimmte Lösung.
- Um die Lösungsmenge des Gleichungssystems (19) zu
beschreiben, betrachten wir den Begriff der verallgemeinerten
inversen Matrix.
- Definition
 Eine
Eine 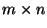 Matrix
Matrix
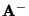 heißt
verallgemeinerte Inverse der
heißt
verallgemeinerte Inverse der 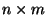 Matrix
Matrix
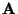 ,
falls
,
falls
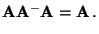 |
(20) |
Um zu zeigen, daß es immer eine Lösung
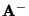 der
Definitionsgleichung (20) gibt, benutzen wir die
folgende allgemeine Matrix-Darstellungsformel, die wir hier ohne
Beweis angeben.
der
Definitionsgleichung (20) gibt, benutzen wir die
folgende allgemeine Matrix-Darstellungsformel, die wir hier ohne
Beweis angeben.
Mit Hilfe von Lemma 4.1 kann man nun zeigen, wie man
zu Lösungen
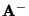 von (20) gelangen kann.
von (20) gelangen kann.
Lemma 4.2
Sei
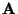
eine
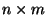
Matrix mit
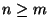
und
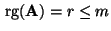
. Dann gibt es für jedes
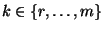
eine
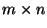
Matrix
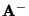
mit
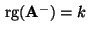
, die der
Gleichung
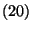
genügt.
- Beweis
-
Außerdem sind die folgenden Eigenschaften der verallgemeinerten
Inversen nützlich.
- Beweis
-
- Definitionsgemäß gilt für die verallgemeinerte Inverse, daß
- Hieraus und aus der Symmetrie der Matrix
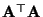 ergibt
sich, daß
ergibt
sich, daß
d.h. die transponierte Matrix
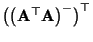 ist ebenfalls
eine verallgemeinerte Inverse von
ist ebenfalls
eine verallgemeinerte Inverse von
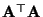 .
.
- Um die zweite Teilaussage (23) zu beweisen,
betrachten wir die Matrix
- Dann gilt
- Hieraus folgt, daß
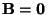 .
.

In der Theorie linearer algebraischer Gleichungssysteme wird
gezeigt, daß die Lösungsmenge der Normalengleichungen
(19) die folgende Gestalt besitzt.
Theorem 4.3
Die allgemeine Lösung
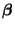
der Normalengleichungen
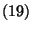
hat die Form
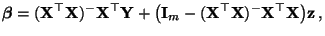 |
(24) |
wobei
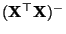
eine beliebige Lösung der Gleichung
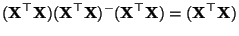 |
(25) |
und
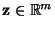
ein beliebiger
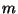
-dimensionaler Vektor ist.
- Beweis
-
- Durch Einsetzen von (24) in die linke Seite der
Normalengleichungen (19) erkennt man mühelos, daß
durch (24) eine Lösung von (19)
gegeben ist, denn es gilt
wobei sich die letzte Gleichheit aus Lemma 4.3
ergibt.
- Der Beweis, daß durch den Ansatz (24) sämtliche Lösungen von (19) gegeben sind, wird in
den Übungen diskutiert, vgl. Übungsaufgabe 10.3.

- Beachte
-
- Aus (24) ergibt sich insbesondere, daß
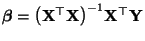 die
eindeutig bestimmte Lösung von (19) ist, falls
die
eindeutig bestimmte Lösung von (19) ist, falls
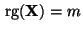 .
.
- Denn dann gilt auch
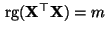 , und
, und
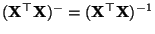 ist die
(eindeutig bestimmte) Inverse von
ist die
(eindeutig bestimmte) Inverse von
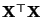 .
.
- Beispiel
 (einfaktorielle Varianzanalyse)
(einfaktorielle Varianzanalyse)
- Zur Erinnerung: Im reparametrisierten Modell der
einfaktoriellen Varianzanalyse (vgl. Fall
 des in
Abschnitt 4.1.1 betrachteten Beispiels) ist die
Designmatrix gegeben durch die
des in
Abschnitt 4.1.1 betrachteten Beispiels) ist die
Designmatrix gegeben durch die
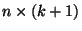 Matrix
Matrix
 |
(26) |
und der Parametervektor
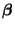 ist gegeben durch
ist gegeben durch
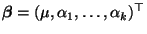 .
.
- Man kann sich leicht überlegen (vgl. Übungsaufgabe 11.1), daß
 |
(27) |
und daß eine verallgemeinerte Inverse von
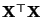 gegeben ist durch
gegeben ist durch
 |
(28) |
- Die Normalengleichungen (19), d.h.
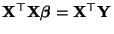 , besitzen somit die
folgende Gestalt:
, besitzen somit die
folgende Gestalt:
- Wenn wir die Lösungen dieses Gleichungssystems lediglich in dem
eingeschränkten Parameterraum
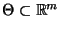 suchen,
wobei
suchen,
wobei
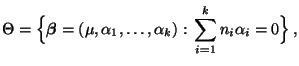 |
(29) |
dann ergibt sich die (eindeutig bestimmte) Lösung
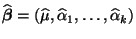 mit
mit
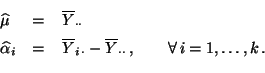 |
(30) |
- Man kann sich leicht überlegen (vgl. Übungsaufgabe 11.1), daß die
in (30) gegebene Lösung
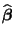 der
Normalengleichungen
der
Normalengleichungen
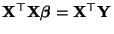
- die Gestalt
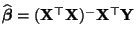 hat, wobei die verallgemeinerte Inverse
hat, wobei die verallgemeinerte Inverse
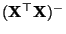 durch (28) gegeben ist, und
durch (28) gegeben ist, und
- ein erwartungstreuer Schätzer für
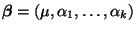 bezüglich des
eingeschränkten Parameterraumes
bezüglich des
eingeschränkten Parameterraumes 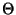 ist, der in
(29) gegeben ist.
ist, der in
(29) gegeben ist.
- Ohne die in (29) betrachtete Nebenbedingung gibt es
jedoch keinen MKQ-Schätzer für
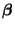 , der gleichzeitig
erwartungstreu ist, vgl. die Diskussion am Ende von
Abschnitt 4.2.1.
, der gleichzeitig
erwartungstreu ist, vgl. die Diskussion am Ende von
Abschnitt 4.2.1.
Für das in (1) - (3) gegebene
lineare Modell mit allgemeiner Designmatrix
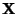 betrachten wir
nun eine beliebige verallgemeinerte Inverse
betrachten wir
nun eine beliebige verallgemeinerte Inverse
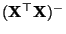 der
der 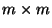 Matrix
Matrix
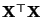 und konstruieren eine
Klasse von MKQ-Schätzern für den Parametervektor
und konstruieren eine
Klasse von MKQ-Schätzern für den Parametervektor
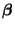 .
.
Theorem 4.4

Sei
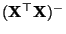
eine beliebige Lösung der Gleichung
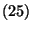
. Dann minimiert die Stichprobenfunktion
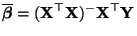 |
(31) |
den in
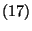
gegebenen mittleren quadratischen
Fehler
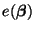
, d.h.,
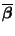
ist ein
MKQ-Schätzer für
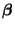
.
- Beweis
-
- Für jeden
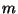 -dimensionalen Vektor
-dimensionalen Vektor
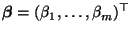 gilt
gilt
weil
und
wobei sich die letzte Gleichheit aus Lemma 4.3
ergibt.

Aus den Modellannahmen (3) über die Störgrößen
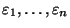 und aus den allgemeinen Rechenregeln für den
Erwartungswert bzw. die Kovarianz von reellwertigen
Zufallsvariablen (vgl. die Abschnitte WR-4.1.3 bzw. WR-4.3.2)
ergibt sich, daß Erwartungswertvektor und Kovarianzmatrix des
MKQ-Schätzers
und aus den allgemeinen Rechenregeln für den
Erwartungswert bzw. die Kovarianz von reellwertigen
Zufallsvariablen (vgl. die Abschnitte WR-4.1.3 bzw. WR-4.3.2)
ergibt sich, daß Erwartungswertvektor und Kovarianzmatrix des
MKQ-Schätzers
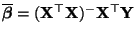 die
folgende Form haben.
die
folgende Form haben.
- Beweis
-
- Aus
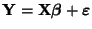 und
und
 ergibt
sich, daß
ergibt
sich, daß
- Außerdem gilt für beliebige
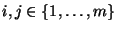

- Beachte
-
- Aus (32) ergibt sich insbesondere, daß der in
(31) gegebene MKQ-Schätzer
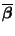 für
für
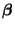 nicht erwartungstreu ist.
nicht erwartungstreu ist.
- Um dies zu zeigen, ist die folgende Eigenschaft des Ranges von
Matrixprodukten nützlich, die wir hier ohne Beweis erwähnen.
Lemma 4.4
Seien
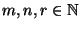
beliebige natürliche Zahlen, und seien
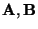
beliebige
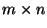
bzw.
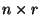
Matrizen.
Dann gilt
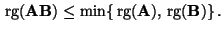 |
(34) |
Wir zeigen nun, daß es keinen MKQ-Schätzer für
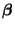 gibt, der gleichzeitig erwartungstreu ist. Insbesondere ist der in
(31) gegebene MKQ-Schätzer
gibt, der gleichzeitig erwartungstreu ist. Insbesondere ist der in
(31) gegebene MKQ-Schätzer
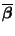 für
für
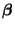 nicht erwartungstreu.
nicht erwartungstreu.




Next: Schätzbare Funktionen
Up: Schätzung der Modellparameter
Previous: Schätzung der Modellparameter
Contents
Ursa Pantle
2003-03-10
![]() der
Definitionsgleichung (20) gibt, benutzen wir die
folgende allgemeine Matrix-Darstellungsformel, die wir hier ohne
Beweis angeben.
der
Definitionsgleichung (20) gibt, benutzen wir die
folgende allgemeine Matrix-Darstellungsformel, die wir hier ohne
Beweis angeben.
![]() von (20) gelangen kann.
von (20) gelangen kann.
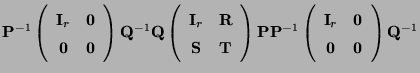
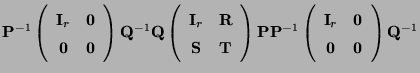
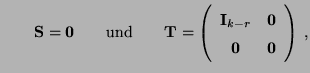
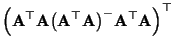
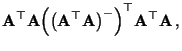
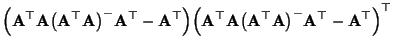
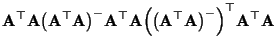
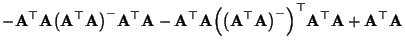
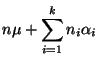
![]() betrachten wir
nun eine beliebige verallgemeinerte Inverse
betrachten wir
nun eine beliebige verallgemeinerte Inverse
![]() der
der ![]() Matrix
Matrix
![]() und konstruieren eine
Klasse von MKQ-Schätzern für den Parametervektor
und konstruieren eine
Klasse von MKQ-Schätzern für den Parametervektor
![]() .
.
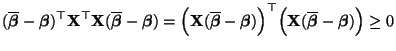
![]() und aus den allgemeinen Rechenregeln für den
Erwartungswert bzw. die Kovarianz von reellwertigen
Zufallsvariablen (vgl. die Abschnitte WR-4.1.3 bzw. WR-4.3.2)
ergibt sich, daß Erwartungswertvektor und Kovarianzmatrix des
MKQ-Schätzers
und aus den allgemeinen Rechenregeln für den
Erwartungswert bzw. die Kovarianz von reellwertigen
Zufallsvariablen (vgl. die Abschnitte WR-4.1.3 bzw. WR-4.3.2)
ergibt sich, daß Erwartungswertvektor und Kovarianzmatrix des
MKQ-Schätzers
![]() die
folgende Form haben.
die
folgende Form haben.
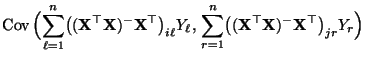
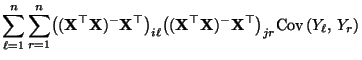
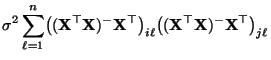
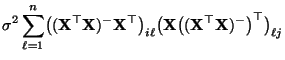
![]() gibt, der gleichzeitig erwartungstreu ist. Insbesondere ist der in
(31) gegebene MKQ-Schätzer
gibt, der gleichzeitig erwartungstreu ist. Insbesondere ist der in
(31) gegebene MKQ-Schätzer
![]() für
für
![]() nicht erwartungstreu.
nicht erwartungstreu.