Next: Beste lineare erwartungstreue Schätzer;
Up: Schätzung der Modellparameter
Previous: Methode der kleinsten Quadrate;
Contents
Schätzbare Funktionen
- In Abschnitt 4.2.1 hatten wir gezeigt, daß es im
linearen Modell ohne Nebenbedingungen keinen MKQ-Schätzer für
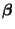 gibt, der gleichzeitig erwartungstreu ist, falls die
Designmatrix
gibt, der gleichzeitig erwartungstreu ist, falls die
Designmatrix
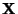 keinen vollen Rang besitzt,
keinen vollen Rang besitzt,
- Anstelle des Vektors
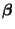 betrachtet man deshalb eine Klasse
von (reellwertigen) linearen Funktionen
betrachtet man deshalb eine Klasse
von (reellwertigen) linearen Funktionen
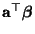 des
Parametervektors
des
Parametervektors
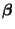 , für die erwartungstreue MKQ-Schätzer
konstruiert werden können.
, für die erwartungstreue MKQ-Schätzer
konstruiert werden können.
- Mit anderen Worten: Anstelle der (vektoriellen)
Lineartransformation
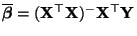 der
Zufallsstichprobe
der
Zufallsstichprobe
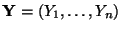 betrachtet man eine
Klasse von (reellwertigen) linearen Funktionen
betrachtet man eine
Klasse von (reellwertigen) linearen Funktionen
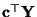 von
von
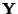 , die als Schätzer von
, die als Schätzer von
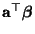 aufgefaßt
werden.
aufgefaßt
werden.
- Dies führt zu der folgenden Begriffsbildung.
- Definition
-
- Beispiel
 (einfaktorielle Varianzanalyse)
(einfaktorielle Varianzanalyse)
- Beispiel
 (zweifaktorielle Varianzanalyse mit balancierten Teilstichproben)
(zweifaktorielle Varianzanalyse mit balancierten Teilstichproben)
- Für das in Abschnitt 4.1.2 eingeführte Modell der
zweifaktoriellen Varianzanalyse mit balancierten Teilstichproben
besitzen die Normalengleichungen (19) die folgende
Gestalt, vgl. Übungsaufgabe 11.2:
- Unter Berücksichtigung der Nebenbedingungen (11)
ist dieses Gleichungssystem eindeutig lösbar. Mit anderen Worten:
Wenn nur Parametervektoren
aus dem eingeschränkten Parameterraum
betrachten werden, dann ergibt sich die eindeutig bestimmte Lösung
der Normalengleichungen, wobei
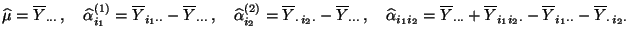 |
(36) |
für beliebige
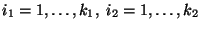 .
.
- Man kann zeigen (vgl. Übungsaufgabe 11.2), daß die in
(36) gegebene Lösung
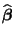 der
Normalengleichungen die Gestalt
der
Normalengleichungen die Gestalt
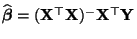 hat, wobei
hat, wobei
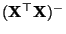 eine verallgemeinerte Inverse von
eine verallgemeinerte Inverse von
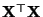 ist und
ist und
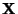 die Designmatrix des
zweifaktoriellen Varianzanalyse-Modells mit balancierten
Teilstichproben ist.
die Designmatrix des
zweifaktoriellen Varianzanalyse-Modells mit balancierten
Teilstichproben ist.
- Beachte: Die Stichprobenfunktion
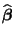 wurde
bereits in Theorem 4.1 diskutiert, wobei gezeigt
wurde, daß
wurde
bereits in Theorem 4.1 diskutiert, wobei gezeigt
wurde, daß
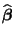 ein erwartungstreuer Schätzer für
ein erwartungstreuer Schätzer für
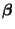 bezüglich des eingeschränkten Parameterraumes
bezüglich des eingeschränkten Parameterraumes 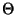 ist.
ist.
- Außerdem kann man zeigen, daß die linearen Funktionen
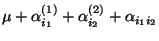 des
Parametervektors
des
Parametervektors
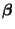 für beliebige
für beliebige
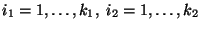 im Sinne der Definitionsgleichung
(35) (d.h. ohne Berücksichtigung der
Nebenbedingungen (11)) erwartungstreu schätzbar
sind.
im Sinne der Definitionsgleichung
(35) (d.h. ohne Berücksichtigung der
Nebenbedingungen (11)) erwartungstreu schätzbar
sind.
- Im Modell der zweifaktoriellen Varianzanalyse ohne
Wechselwirkungen, d.h.
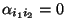 für beliebige
für beliebige
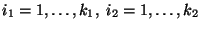 , sind auch
, sind auch
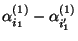 für beliebige
für beliebige
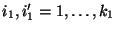 mit
mit
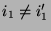 bzw.
bzw.
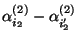 für beliebige
für beliebige
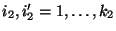 mit
mit
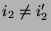 erwartungstreu schätzbar.
erwartungstreu schätzbar.
Wir leiten nun zwei allgemeine Kriterien für die
erwartungstreue Schätzbarkeit von linearen Funktionen
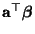 des Parametervektors
des Parametervektors
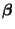 her.
her.
Theorem 4.6
Die lineare Funktion
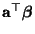
des Parametervektors
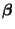
ist genau dann erwartungstreu schätzbar, wenn eine der
folgenden beiden Bedingungen erfüllt ist:
- 1.
- Es gibt einen
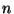 -dimensionalen Vektor
-dimensionalen Vektor
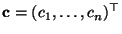 , so daß
, so daß
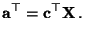 |
(37) |
- 2.
- Der Vektor
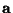 genügt dem folgenden Gleichungssystem:
genügt dem folgenden Gleichungssystem:
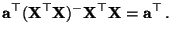 |
(38) |
- Beweis
-
- Beachte
-
- Beweis
-
- Beachte
-
- Der in (41) eingeführte Begriff des projizierten
Parametervektors
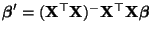 hängt
mit dem Begriff der (nichtnotwendig orthogonalen) Projektion von
Vektorräumen auf Unterräume zusammen, vgl. auch
Abschnitt 3.1.2, wo der Spezialfall der
Orthogonalprojektion diskutiert wurde.
hängt
mit dem Begriff der (nichtnotwendig orthogonalen) Projektion von
Vektorräumen auf Unterräume zusammen, vgl. auch
Abschnitt 3.1.2, wo der Spezialfall der
Orthogonalprojektion diskutiert wurde.
- Und zwar seien
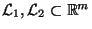 lineare Unterräume
des
lineare Unterräume
des
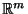 , so daß sich
, so daß sich
-
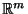 als direkte Summe
als direkte Summe
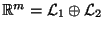 ausdrücken und
ausdrücken und
- jedes
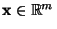 auf eindeutige Weise in
auf eindeutige Weise in
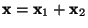 mit
mit
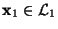 und
und
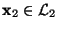 zerlegen läßt.
zerlegen läßt.
- Die Abbildung
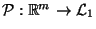 mit
mit
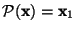 heißt dann Projektion von
heißt dann Projektion von
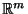 auf den linearen Unterraum
auf den linearen Unterraum
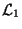 entlang des linearen Unterraumes
entlang des linearen Unterraumes
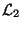 .
.
- In Verallgemeinerung von Lemma 3.5 gilt die folgende
Charakterisierung von Projektionsoperatoren, die wir hier ohne
Beweis erwähnen.
Lemma 4.5

Die
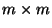
Matrix
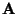
ist genau dann eine Projektion des
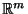
auf den linearen Unterraum
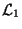
, wenn
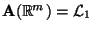
und
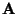
idempotent ist.
- Beachte
-
- Die Matrix
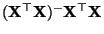 , die in der
Definitionsgleichung (41) des projizierten
Parametervektors
, die in der
Definitionsgleichung (41) des projizierten
Parametervektors
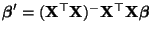 betrachtet wird, ist offenbar idempotent.
betrachtet wird, ist offenbar idempotent.
- Aus Lemma 4.5 ergibt sich somit, daß
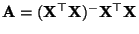 ein (nichtnotwendig
orthogonaler) Projektionsoperator des
ein (nichtnotwendig
orthogonaler) Projektionsoperator des
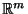 auf den linearen
Unterraum
auf den linearen
Unterraum
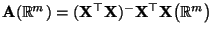 ist.
ist.




Next: Beste lineare erwartungstreue Schätzer;
Up: Schätzung der Modellparameter
Previous: Methode der kleinsten Quadrate;
Contents
Ursa Pantle
2003-03-10
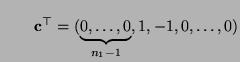
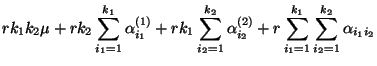
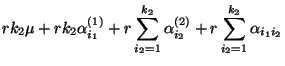
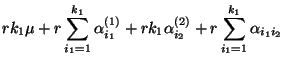
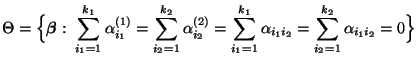
![]() des Parametervektors
des Parametervektors
![]() her.
her.