



Next: Verteilungs- und Unabhängigkeitseigenschaften der
Up: Normalverteilte Störgrößen
Previous: Normalverteilte Störgrößen
Contents
Maximum-Likelihood-Schätzer
- Beachte
-
- Beweis
-
- Aus Lemma 4.3 ergibt sich, daß
- In Lemma 4.3 hatten wir gezeigt, daß
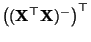 eine verallgemeinerte
Inverse von
eine verallgemeinerte
Inverse von
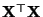 ist. Somit ergibt sich aus
Lemma 4.6, daß
ist. Somit ergibt sich aus
Lemma 4.6, daß
- Damit ist die erste Teilaussage bewiesen. Um die zweite
Teilaussage zu beweisen, genügt es zu beachten, daß
wobei sich die vorletzte Gleichheit aus Lemma 4.3
ergibt (vgl. (39) im Beweis von
Theorem 4.6).
- Um die dritte Teilaussage zu beweisen, überzeugen wir uns zunächst
davon,
- daß
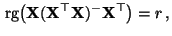 |
(54) |
denn aus Lemma 4.3 und aus Lemma 4.4
ergibt sich, daß
- und daß
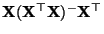 eine idempotente
Matrix ist, denn aus Lemma 4.3 ergibt sich, daß
eine idempotente
Matrix ist, denn aus Lemma 4.3 ergibt sich, daß
- Außerdem kann man zeigen, daß
-
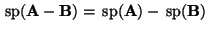 für beliebige
für beliebige
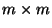 Matrizen
Matrizen
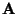 und
und
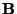 ,
,
-
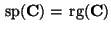 für jede idempotente und symmetrische
für jede idempotente und symmetrische
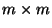 Matrix
Matrix
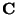 .
.
- Hieraus und aus (54) folgt, daß

Mit Hilfe von Lemma 4.7 können wir nun den
Erwartungswert des ML-Schätzers
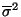 bestimmen.
bestimmen.
- Beweis
-
- Aus (52) - (53) und aus
Lemma 4.7 ergibt sich, daß
wobei
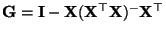 .
.

- Beachte
 Wegen Theorem 4.10 wird anstelle
des ML-Schätzers
Wegen Theorem 4.10 wird anstelle
des ML-Schätzers
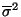 der folgende erwartungstreue
Schätzer
der folgende erwartungstreue
Schätzer 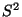 für
für 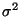 betrachtet:
betrachtet:
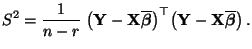 |
(56) |




Next: Verteilungs- und Unabhängigkeitseigenschaften der
Up: Normalverteilte Störgrößen
Previous: Normalverteilte Störgrößen
Contents
Ursa Pantle
2003-03-10
![]() bestimmen.
bestimmen.