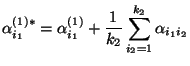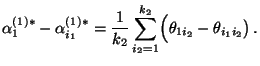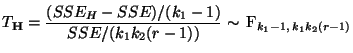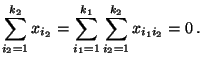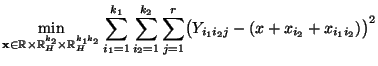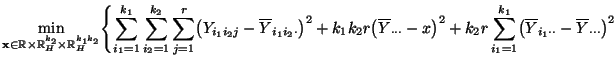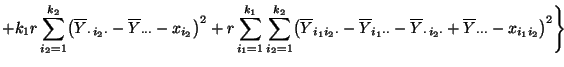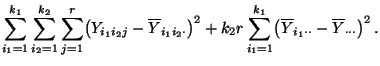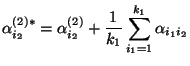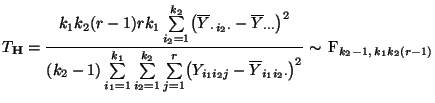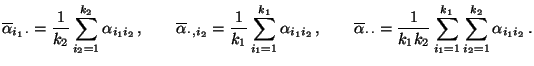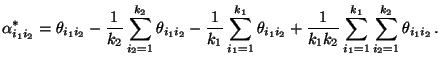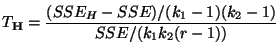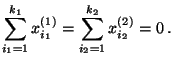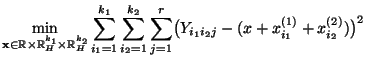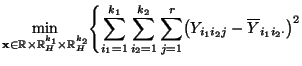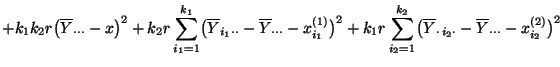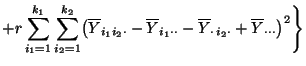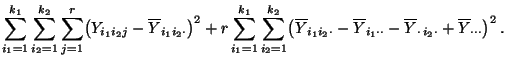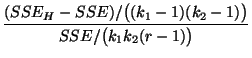F-Tests für die zweifaktorielle Varianzanalyse

Next: Zweifaktorielle Varianzanalyse mit hierarchischer Up: Beispiele Previous: F-Test der ANOVA-Nullhypothese; einfaktorielle Contents

F-Tests für die zweifaktorielle Varianzanalyse

Wir konstruieren nun F-Tests für das in Abschnitt 4.1.2 eingeführte Modell der zweifaktoriellen Varianzanalyse mit balancierten Teilstichproben, d.h.,

der Parametervektor ${\boldsymbol {\beta }}$ hat die Form

$\displaystyle {\boldsymbol{\beta}}=\bigl(\mu,\alpha^{(1)}_1,\ldots, \alpha^{(1... ...,\ldots, \alpha^{(2)}_{k_2},\alpha_{11},\ldots,\alpha_{k_1k_2}\bigr)^\top\,,$
die Designmatrix ${\mathbf{X}}$ hat die Dimension $n\times m$ , wobei und ,
die Eintragungen von ${\mathbf{X}}$ bestehen nur aus Nullen und Einsen, und es gilt ${\,{\rm rg}}({\mathbf{X}})=k_1k_2<m$ .

Signifikanz der Einflußfaktoren

Wir konstruieren zunächst einen Test zur Untersuchung der Frage, ob die Stufen des ersten Einflußfaktors signifikant sind. Hierfür prüfen wir die Hypothese, ob die Effekte

$\displaystyle \alpha_{i_1}^{(1)*}=\alpha_{i_1}^{(1)}+\frac{1}{k_2}\sum\limits_{i_2=1}^{k_2}\alpha_{i_1i_2}$
des ersten Einflußfaktors, gemittelt über sämtliche Stufen des zweiten Einflußfaktors, gleich sind.
Mit anderen Worten: Wir testen wir die Hypothese

$\displaystyle H_0: \alpha_{1}^{(1)*}-\alpha_{i_1}^{(1)*}=0\quad\forall\, i_1\in\{1,\ldots,k_1\}$ versus $\displaystyle \qquad H_1: \alpha_{1}^{(1)*}-\alpha_{i_1}^{(1)*}\not=0$ $\displaystyle \mbox{für ein $i_1\in\{1,\ldots,k_1\}$}$ $\displaystyle \,.$
Dabei kann man zeigen (vgl. Übungsaufgabe 12.3), daß die Nullhypothese die Form 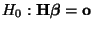hat, wobei
- ${\mathbf{H}}$ eine $(k_1-1)\times m$ Matrix mit vollem Zeilenrang ${\,{\rm rg}}({\mathbf{H}})=k_1-1$ ist und
- sämtliche Komponenten des Vektors ${\mathbf{H}}{\boldsymbol{\beta}}$ schätzbare Funktionen von ${\boldsymbol {\beta }}$ sind, denn es gilt
  
  $\displaystyle \alpha_{1}^{(1)*}-\alpha_{i_1}^{(1)*}=\frac{1}{k_2} \sum\limits_{i_2=1}^{k_2}\Bigl(\theta_{1i_2}-\theta_{i_1i_2}\bigr)\,.$
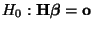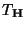Zur Verifizierung der Hypothese $H_0:{\mathbf{H}}{\boldsymbol{\beta}}={\mathbf{o}}$ kann somit erneut die in Theorem 4.14 betrachtete Testgröße $T_{\mathbf{H}}$ verwendet werden, wobei

$\displaystyle T_{\mathbf{H}}=\frac{(SSE_H-SSE)/(k_1-1)}{SSE/(k_1k_2(r-1))}\sim\,{\rm F}_{k_1-1,\,k_1k_2(r-1)}$
mit

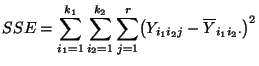$\displaystyle SSE=\sum\limits_{i_1=1}^{k_1}\sum\limits_{i_2=1}^{k_2}\sum\limits_{j=1}^r \bigl(Y_{i_1i_2j}-\overline Y_{i_1i_2\cdot}\bigr)^2$ (82)

und

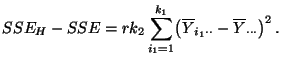$\displaystyle SSE_H-SSE=rk_2 \sum\limits_{i_1=1}^{k_1} \bigl(\overline Y_{i_1\cdot\cdot}- \overline Y_{\cdot\cdot\cdot}\bigr)^2\,.$ (83)
Dabei lassen sich die Formeln (82) und (83) für die in (68) bzw. (69) definierten Quadratsummen 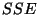und 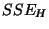auf ähnliche Weise wie in Abschnitt 4.4.1 herleiten.
Und zwar ergibt sich (82) mit der gleichen Minimierungstechnik, die bei der direkten Herleitung von (80) verwendet wurde. Darüber hinaus läßt sich die Quadratsumme 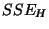wie folgt bestimmen.
Die Menge 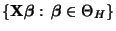$% latex2html id marker 45774 $ \{{\mathbf{X}}{\boldsymbol{\beta}}:\,{\boldsymbol{\beta}}\in\Theta_H\}$$ läßt sich durch die Menge 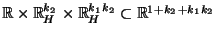$\mathbb{R}\times\mathbb{R}^{k_2}_H\times\mathbb{R}^{k_1k_2}_H\subset\mathbb{R}^{1+k_2+k_1k_2}$ derjenigen Vektoren 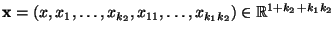${\mathbf{x}}=(x,x_1,\ldots,x_{k_2},x_{11},\ldots,x_{k_1k_2})\in\mathbb{R}^{1+k_2+k_1k_2}$ beschreiben, die den folgenden Bedingungen genügen:

$\displaystyle \sum\limits_{i_2=1}^{k_2} x_{i_2}=\sum\limits_{i_1=1}^{k_1}\sum\limits_{i_2=1}^{k_2} x_{i_1i_2}=0\,.$
Somit gilt

$\displaystyle SSE_H$ $\displaystyle =$ $% latex2html id marker 45787 $\displaystyle ({\mathbf{Y}}-{\mathbf{X}}\overline{... ...\in\Theta_H}\bigl\Vert{\mathbf{Y}}-{\mathbf{X}}{\boldsymbol{\beta}}\bigr\Vert^2$$

$\displaystyle =$ $\displaystyle \min\limits_{{\mathbf{x}}\in\mathbb{R}\times\mathbb{R}^{k_2}_H\ti... ..._2=1}^{k_2} \sum\limits_{j=1}^r\bigl(Y_{i_1i_2j}-(x+x_{i_2}+x_{i_1i_2})\bigr)^2$

$\displaystyle =$ $\displaystyle \min\limits_{{\mathbf{x}}\in\mathbb{R}\times\mathbb{R}^{k_2}_H\ti... ...1}^{k_1}\bigl(\overline Y_{i_1\cdot\cdot}-\overline Y_{\cdot\cdot\cdot}\bigr)^2$

$\displaystyle + k_1r \sum\limits_{i_2=1}^{k_2}\bigl(\overline Y_{\cdot\,i_2\cdo... ... Y_{\cdot\,i_2\cdot}+\overline Y_{\cdot\cdot\cdot}-x_{i_1i_2} \bigr)^2 \Biggr\}$

$\displaystyle =$ $\displaystyle \sum\limits_{i_1=1}^{k_1}\sum\limits_{i_2=1}^{k_2}\sum\limits_{j=... ...{k_1}\bigl(\overline Y_{i_1\cdot\cdot}-\overline Y_{\cdot\cdot\cdot}\bigr)^2\,.$
Hieraus und aus (82) ergibt sich nun (83).

Beachte

Auf die gleiche Weise ergibt sich ein Test, um zu prüfen, ob die Stufen des zweiten Einflußfaktors signifikant sind. Dabei prüfen wir die Hypothese, ob die Effekte

$\displaystyle \alpha_{i_2}^{(2)*}=\alpha_{i_2}^{(2)}+\frac{1}{k_1}\sum\limits_{i_1=1}^{k_1}\alpha_{i_1i_2}$
des zweiten Einflußfaktors, gemittelt über sämtliche Stufen des ersten Einflußfaktors, gleich sind.
Wir testen also die Hypothese

$\displaystyle H_0: \alpha_{1}^{(2)*}-\alpha_2^{(2)*}=0\,,\,\ldots\,,\,\alpha_{1}^{(2)*}-\alpha_{k_2}^{(2)*}=0$ versus $\displaystyle \quad H_1: \alpha_{1}^{(2)*}-\alpha_{i_2}^{(2)*}\not=0$ $\displaystyle \mbox{für ein $i_2\in\{1,\ldots,k_2\}$}$ $\displaystyle \,.$
Als Testgröße ergibt sich in diesem Fall:

$\displaystyle T_{\mathbf{H}}=\frac{k_1k_2(r-1)rk_1 \sum\limits_{i_2=1}^{k_2} \... ..._1i_2j}-\overline Y_{i_1i_2\cdot}\bigr)^2}\sim\,{\rm F}_{k_2-1,\,k_1k_2(r-1)}$

Wechselwirkungen zwischen den beiden Einflußfaktoren

Wir konstruieren nun einen Test, um zu prüfen, ob es signifikante Wechselwirkungen zwischen den beiden Einflußfaktoren gibt. Hierfür testen wir die Hypothese

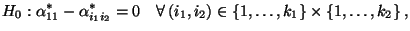$\displaystyle H_0:\alpha^*_{11}-\alpha^*_{i_1i_2}=0\quad\forall\, (i_1,i_2)\in\{1,\ldots,k_1\}\times\{1,\ldots,k_2\}\,,$ (84)

wobei

$\displaystyle \alpha^*_{i_1i_2}=\alpha_{i_1i_2}-\overline\alpha_{i_1\,\cdot} -\overline\alpha_{\cdot\,i_2} +\overline\alpha_{\cdot\,\cdot}$
und

$\displaystyle \overline\alpha_{i_1\,\cdot}=\frac{1}{k_2}\sum\limits_{i_2=1}^{k_... ...k_1k_2}\sum\limits_{i_1=1}^{k_1}\sum\limits_{i_2=1}^{k_2} \alpha_{i_1i_2}\,.$
Man kann zeigen (vgl. Übungsaufgabe 12.3), daß sich die in (84) betrachtete Hypothese in der Form 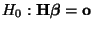schreiben läßt, wobei
- ${\mathbf{H}}$ eine $(k_1-1)(k_2-1)\times m$ Matrix mit vollem Zeilenrang ${\,{\rm rg}}({\mathbf{H}})=(k_1-1)(k_2-1)$ ist und
- sämtliche Komponenten des Vektors ${\mathbf{H}}{\boldsymbol{\beta}}$ schätzbare Funktionen von ${\boldsymbol {\beta }}$ sind, denn es gilt
  
  $\displaystyle \alpha_{i_1i_2}^*=\theta_{i_1i_2}-\frac{1}{k_2} \sum\limits_{i_2... ...k_1k_2}\sum\limits_{i_1=1}^{k_1} \sum\limits_{i_2=1}^{k_2}\theta_{i_1i_2}\,.$
Zur Verifizierung der Hypothese 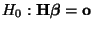$H_0:{\mathbf{H}}{\boldsymbol{\beta}}={\mathbf{o}}$ kann somit die in Theorem 4.14 betrachtete Testgröße

$\displaystyle T_{\mathbf{H}}=\frac{(SSE_H-SSE)/(k_1-1)(k_2-1)}{SSE/(k_1k_2(r-1))}$
verwendet werden, wobei 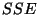so wie bisher durch (82) gegeben ist, während sich die Quadratsumme 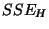aus den folgenden Überlegungen ergibt.
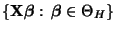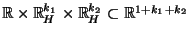Die Menge $% latex2html id marker 45841 $ \{{\mathbf{X}}{\boldsymbol{\beta}}:\,{\boldsymbol{\beta}}\in\Theta_H\}$$ läßt sich durch die Menge $\mathbb{R}\times\mathbb{R}^{k_1}_H\times\mathbb{R}^{k_2}_H\subset\mathbb{R}^{1+k_1+k_2}$ derjenigen Vektoren

$\displaystyle {\mathbf{x}}=(x,x^{(1)}_1,\ldots,x^{(1)}_{k_1},x^{(2)}_1,\ldots,x^{(2)}_{k_2})\in\mathbb{R}^{1+k_1+k_2}$
beschreiben, die den folgenden Bedingungen genügen:

$\displaystyle \sum\limits_{i_1=1}^{k_1} x^{(1)}_{i_1}=\sum\limits_{i_2=1}^{k_2} x^{(2)}_{i_2}=0\,.$
Somit gilt

$\displaystyle SSE_H$ $\displaystyle =$ $% latex2html id marker 45854 $\displaystyle ({\mathbf{Y}}-{\mathbf{X}}\overline{... ...\in\Theta_H}\bigl\Vert{\mathbf{Y}}-{\mathbf{X}}{\boldsymbol{\beta}}\bigr\Vert^2$$

$\displaystyle =$ $\displaystyle \min\limits_{{\mathbf{x}}\in\mathbb{R}\times\mathbb{R}^{k_1}_H\ti... ...2} \sum\limits_{j=1}^r\bigl(Y_{i_1i_2j}-(x+x_{i_1}^{(1)}+x_{i_2}^{(2)})\bigr)^2$

$\displaystyle =$ $\displaystyle \min\limits_{{\mathbf{x}}\in\mathbb{R}\times\mathbb{R}^{k_1}_H\ti... ...1}^{k_2}\sum\limits_{j=1}^r \bigl(Y_{i_1i_2j}-\overline Y_{i_1i_2\cdot}\bigr)^2$

$\displaystyle + k_1k_2r\bigl(\overline Y_{\cdot\cdot\cdot}-x\bigr)^2+k_2r\sum\l... ...erline Y_{\cdot\,i_2\cdot}-\overline Y_{\cdot\cdot\cdot}-x^{(2)}_{i_2} \bigr)^2$

$\displaystyle +r\sum\limits_{i_1=1}^{k_1}\sum\limits_{i_2=1}^{k_2} \bigl(\overl... ...}-\overline Y_{\cdot\,i_2\cdot}+\overline Y_{\cdot\cdot\cdot} \bigr)^2 \Biggr\}$

$\displaystyle =$ $\displaystyle \sum\limits_{i_1=1}^{k_1}\sum\limits_{i_2=1}^{k_2}\sum\limits_{j=... ...cdot} -\overline Y_{\cdot\, i_2\cdot}+\overline Y_{\cdot\cdot\cdot} \bigr)^2\,.$
Hieraus und aus (82) folgt, daß

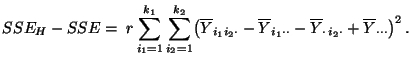$\displaystyle SSE_H-SSE=\;r \sum\limits_{i_1=1}^{k_1}\sum\limits_{i_2=1}^{k_2} ... ...t\cdot}-\overline Y_{\cdot\, i_2\cdot}+\overline Y_{\cdot\cdot\cdot}\bigr)^2\,.$ (85)
Für die in Theorem 4.14 betrachtete Testgröße 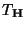$T_{\mathbf{H}}$ gilt also, daß

$\displaystyle T_{\mathbf{H}}$ $\displaystyle =$ $\displaystyle \frac{(SSE_H-SSE)/\bigl((k_1-1)(k_2-1)\bigr)}{SSE/\bigl(k_1k_2(r-1)\bigr)}$

$\displaystyle =$ $\displaystyle \frac{k_1k_2(r-1) r \sum\limits_{i_1=1}^{k_1}\sum\limits_{i_2=1}^... ...erline Y_{i_1i_2\cdot}\bigr)^2} \sim\,{\rm F}_{(k_1-1)(k_2-1),\,k_1k_2(r-1)}\,.$

Next: Zweifaktorielle Varianzanalyse mit hierarchischer Up: Beispiele Previous: F-Test der ANOVA-Nullhypothese; einfaktorielle Contents

Ursa Pantle 2003-03-10

$\displaystyle SSE_H$	$\displaystyle =$	$% latex2html id marker 45787 $\displaystyle ({\mathbf{Y}}-{\mathbf{X}}\overline{... ...\in\Theta_H}\bigl\Vert{\mathbf{Y}}-{\mathbf{X}}{\boldsymbol{\beta}}\bigr\Vert^2$$
	$\displaystyle =$	$\displaystyle \min\limits_{{\mathbf{x}}\in\mathbb{R}\times\mathbb{R}^{k_2}_H\ti... ..._2=1}^{k_2} \sum\limits_{j=1}^r\bigl(Y_{i_1i_2j}-(x+x_{i_2}+x_{i_1i_2})\bigr)^2$
	$\displaystyle =$	$\displaystyle \min\limits_{{\mathbf{x}}\in\mathbb{R}\times\mathbb{R}^{k_2}_H\ti... ...1}^{k_1}\bigl(\overline Y_{i_1\cdot\cdot}-\overline Y_{\cdot\cdot\cdot}\bigr)^2$
		$\displaystyle + k_1r \sum\limits_{i_2=1}^{k_2}\bigl(\overline Y_{\cdot\,i_2\cdo... ... Y_{\cdot\,i_2\cdot}+\overline Y_{\cdot\cdot\cdot}-x_{i_1i_2} \bigr)^2 \Biggr\}$
	$\displaystyle =$	$\displaystyle \sum\limits_{i_1=1}^{k_1}\sum\limits_{i_2=1}^{k_2}\sum\limits_{j=... ...{k_1}\bigl(\overline Y_{i_1\cdot\cdot}-\overline Y_{\cdot\cdot\cdot}\bigr)^2\,.$

$\displaystyle SSE_H$	$\displaystyle =$	$% latex2html id marker 45854 $\displaystyle ({\mathbf{Y}}-{\mathbf{X}}\overline{... ...\in\Theta_H}\bigl\Vert{\mathbf{Y}}-{\mathbf{X}}{\boldsymbol{\beta}}\bigr\Vert^2$$
	$\displaystyle =$	$\displaystyle \min\limits_{{\mathbf{x}}\in\mathbb{R}\times\mathbb{R}^{k_1}_H\ti... ...2} \sum\limits_{j=1}^r\bigl(Y_{i_1i_2j}-(x+x_{i_1}^{(1)}+x_{i_2}^{(2)})\bigr)^2$
	$\displaystyle =$	$\displaystyle \min\limits_{{\mathbf{x}}\in\mathbb{R}\times\mathbb{R}^{k_1}_H\ti... ...1}^{k_2}\sum\limits_{j=1}^r \bigl(Y_{i_1i_2j}-\overline Y_{i_1i_2\cdot}\bigr)^2$
		$\displaystyle + k_1k_2r\bigl(\overline Y_{\cdot\cdot\cdot}-x\bigr)^2+k_2r\sum\l... ...erline Y_{\cdot\,i_2\cdot}-\overline Y_{\cdot\cdot\cdot}-x^{(2)}_{i_2} \bigr)^2$
		$\displaystyle +r\sum\limits_{i_1=1}^{k_1}\sum\limits_{i_2=1}^{k_2} \bigl(\overl... ...}-\overline Y_{\cdot\,i_2\cdot}+\overline Y_{\cdot\cdot\cdot} \bigr)^2 \Biggr\}$
	$\displaystyle =$	$\displaystyle \sum\limits_{i_1=1}^{k_1}\sum\limits_{i_2=1}^{k_2}\sum\limits_{j=... ...cdot} -\overline Y_{\cdot\, i_2\cdot}+\overline Y_{\cdot\cdot\cdot} \bigr)^2\,.$

$\displaystyle T_{\mathbf{H}}$	$\displaystyle =$	$\displaystyle \frac{(SSE_H-SSE)/\bigl((k_1-1)(k_2-1)\bigr)}{SSE/\bigl(k_1k_2(r-1)\bigr)}$
	$\displaystyle =$	$\displaystyle \frac{k_1k_2(r-1) r \sum\limits_{i_1=1}^{k_1}\sum\limits_{i_2=1}^... ...erline Y_{i_1i_2\cdot}\bigr)^2} \sim\,{\rm F}_{(k_1-1)(k_2-1),\,k_1k_2(r-1)}\,.$