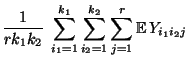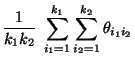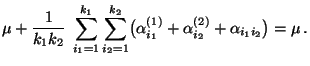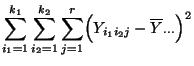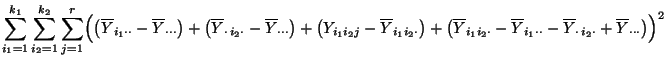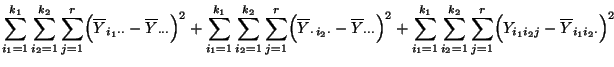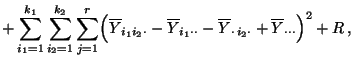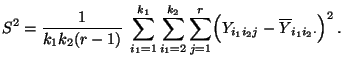Next: Schätzung der Modellparameter
Up: Beispiele: Varianzanalyse als lineares
Previous: Einfaktorielle Varianzanalyse
Contents
Zweifaktorielle Varianzanalyse
- Beachte
-
- Die Darstellung (8) der Stichprobenvariablen
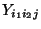 führt zu der gleichen Art eines linearen Modells,
wie es in Fall 1 von Abschnitt 4.1.1 betrachtet wurde.
führt zu der gleichen Art eines linearen Modells,
wie es in Fall 1 von Abschnitt 4.1.1 betrachtet wurde.
- Die Nummern
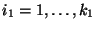 bzw.
bzw.
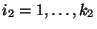 der
Klassen
der
Klassen
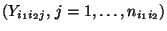 werden erneut als
Stufen des jeweiligen Einflußfaktors gedeutet.
werden erneut als
Stufen des jeweiligen Einflußfaktors gedeutet.
- Die Designmatrix
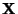 hat dabei die Dimension
hat dabei die Dimension
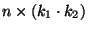 und den vollen Spaltenrang
und den vollen Spaltenrang
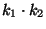 .
.
Wir betrachten eine ähnliche Reparametrisierung der
Erwartungswerte
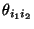 wie in
Abschnitt 4.1.1.
wie in
Abschnitt 4.1.1.
- Dabei betrachten wir lediglich den sogenannten balancierten
Fall, d.h., wir setzen zusätzlich voraus, daß sämtliche
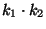 Teilstichproben
Teilstichproben
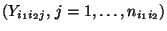 identische Stichprobenumfänge besitzen.
identische Stichprobenumfänge besitzen.
- Es gelte also
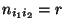 für alle
für alle
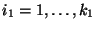 und
und
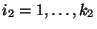 , wobei
, wobei
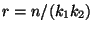 .
.
- Sei nun
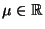 , und für alle
, und für alle
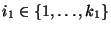 und
und
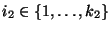 seien
seien
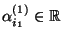 ,
,
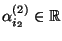 und
und
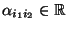 reelle
Zahlen, so daß
reelle
Zahlen, so daß
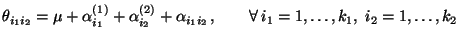 |
(10) |
und
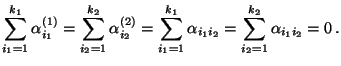 |
(11) |
- Dann läßt sich die Zufallsstichprobe
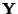 in der Form
in der Form
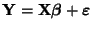 darstellen, wobei
darstellen, wobei
- die Designmatrix
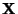 gegeben ist durch eine Matrix der
Dimension
gegeben ist durch eine Matrix der
Dimension
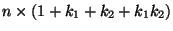 , deren Eintragungen nur aus
Nullen und Einsen bestehen und die keinen vollen Rang hat, und
wobei
, deren Eintragungen nur aus
Nullen und Einsen bestehen und die keinen vollen Rang hat, und
wobei
- der Parametervektor
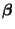 die folgende Form hat:
die folgende Form hat:
- Beachte
-
- Die linearen Nebenbedingungen (11) an die
Komponenten des Parametervektors
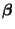 bewirken, ähnlich wie
bei dem in Abschnitt 4.1.1 betrachteten Modell der
einfaktoriellen Varianzanalyse, daß die Darstellung
(10) - (11) der Erwartungswerte
bewirken, ähnlich wie
bei dem in Abschnitt 4.1.1 betrachteten Modell der
einfaktoriellen Varianzanalyse, daß die Darstellung
(10) - (11) der Erwartungswerte
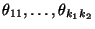 eindeutig ist, vgl.
Übungsaufgabe 10.1b.
eindeutig ist, vgl.
Übungsaufgabe 10.1b.
- Dabei kann
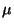 als allgemeines Mittel der Erwartungswerte
als allgemeines Mittel der Erwartungswerte
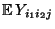 der Stichprobenvariablen
der Stichprobenvariablen
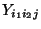 aufgefaßt
werden,
aufgefaßt
werden,
-
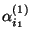 wird Haupteffekt der
wird Haupteffekt der 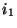 -ten Stufe
des ersten Einflußfaktors genannt,
-ten Stufe
des ersten Einflußfaktors genannt,
-
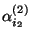 heißt Haupteffekt der
heißt Haupteffekt der 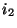 -ten Stufe
des zweiten Einflußfaktors, und
-ten Stufe
des zweiten Einflußfaktors, und
-
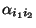 heißt Wechselwirkung zwischen den Stufen
heißt Wechselwirkung zwischen den Stufen
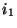 und
und 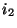 der Stufenkombination
der Stufenkombination 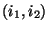 .
.
Zur Konstruktion von Schätzern für die Modellparameter 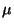 ,
,
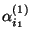 ,
,
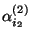 bzw.
bzw.
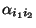 verwenden wir, ähnlich wie in Abschnitt 2.2, die
folgende Notation: Sei
verwenden wir, ähnlich wie in Abschnitt 2.2, die
folgende Notation: Sei
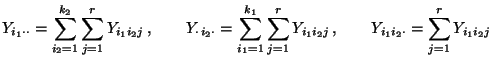 |
(12) |
bzw.
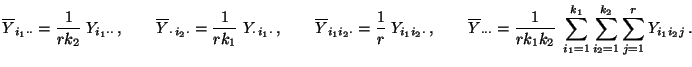 |
(13) |
Theorem 4.1

Es gilt
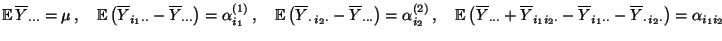 |
(14) |
für beliebige
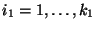
,
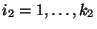
, d.h., durch
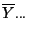
,
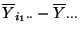
,
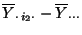
und
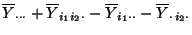
sind
erwartungstreue Schätzer für die Modellparameter
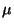
,
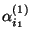
,
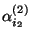
bzw.
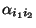
gegeben .
- Beweis
-
- Aus der Definitionsgleichung von
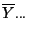 in (13) ergibt sich, daß
in (13) ergibt sich, daß
wobei sich die letzte Gleichheit aus den
Reparametrisierungsbedingungen (11) ergibt.
- Die anderen drei Teilaussagen in (14) lassen sich
auf analoge Weise beweisen.

- Beachte
-
- Die Bedingungen (11), d.h. die Annahme, daß der
Parametervektor
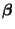 zu einem linearen Unterraum des
zu einem linearen Unterraum des
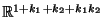 gehört, spielen eine zentrale Rolle im
Beweis von Theorem 4.1.
gehört, spielen eine zentrale Rolle im
Beweis von Theorem 4.1.
- Dabei werden die Aussagen von Theorem 4.1 als
Erwartungstreue der betrachteten Schätzer bezüglich dieses
eingeschränkten Parameterraumes interpretiert.
- Falls jedoch zugelassen wird, daß
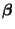 ein beliebiger
Vektor der Dimension
ein beliebiger
Vektor der Dimension
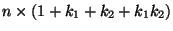 ist, dann gibt es
keinen MKQ-Schätzer für
ist, dann gibt es
keinen MKQ-Schätzer für
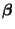 , der gleichzeitig
erwartungstreu ist, vgl. Abschnitt 4.2.1.
, der gleichzeitig
erwartungstreu ist, vgl. Abschnitt 4.2.1.
Wir diskutieren nun noch die folgende Quadratsummenzerlegung, vgl. auch Theorem 2.13, wo
ein ähnliches Resultat für das einfaktorielle
Varianzanalyse-Modell hergeleitet wurde.
- Beweis
 Mit der in (12) bzw. (13)
eingeführten Notation gilt
Mit der in (12) bzw. (13)
eingeführten Notation gilt
wobei genauso wie im Beweis von Theorem 2.13 gezeigt
werden kann, daß die Summe 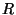 der gemischten Produkte gleich Null
ist.
der gemischten Produkte gleich Null
ist.

- Beachte
-
- Die Quadratsumme auf der linken Seite von (15) kann
als eine Maßzahl für die (Gesamt-) Variabilität der
Stichprobenvariablen
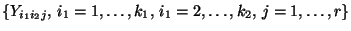 aufgefaßt
werden.
aufgefaßt
werden.
- Die ersten beiden Qúadratsummen auf der rechten Seite von
(15) sind Maßzahlen für die Variabilität zwischen den Stufen des ersten bzw. zweiten Einflußfaktors,
während die dritte Quadratsumme auf der rechten Seite von
(15) eine Maßzahl für die Variabilität innerhalb der Stufenpaare
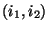 der beiden Einflußfaktoren
ist, die sogenannte Reststreuung.
der beiden Einflußfaktoren
ist, die sogenannte Reststreuung.
- Die vierte Quadratsumme auf der rechten Seite von
(15) ist eine Maßzahl für die Wechselwirkungen zwischen den Komponenten der Stufenpaare
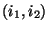 der beiden
Einflußfaktoren.
der beiden
Einflußfaktoren.
- Mit ähnlichen Überlegungen wie im Beweis von
Theorem 4.1 kann man zeigen, daß eine geeignet
normierte Version der Reststreuung ein erwartungstreuer Schätzer
der Varianz
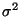 der Störgrößen ist.
der Störgrößen ist.
- Und zwar gilt
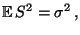 |
(16) |
wobei




Next: Schätzung der Modellparameter
Up: Beispiele: Varianzanalyse als lineares
Previous: Einfaktorielle Varianzanalyse
Contents
Ursa Pantle
2003-03-10
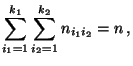
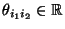 (unbekannte) Parameter sind,
(unbekannte) Parameter sind,
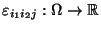 unkorreliert sind mit
unkorreliert sind mit
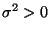 ebenfalls ein unbekannter
Modellparameter ist.
ebenfalls ein unbekannter
Modellparameter ist.
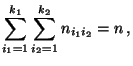
![]() wie in
Abschnitt 4.1.1.
wie in
Abschnitt 4.1.1.
![]() ,
,
![]() ,
,
![]() bzw.
bzw.
![]() verwenden wir, ähnlich wie in Abschnitt 2.2, die
folgende Notation: Sei
verwenden wir, ähnlich wie in Abschnitt 2.2, die
folgende Notation: Sei