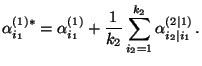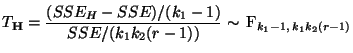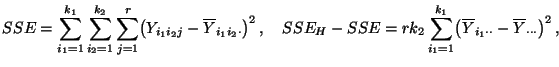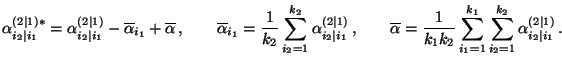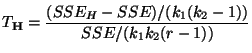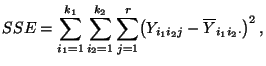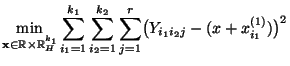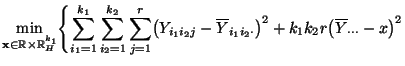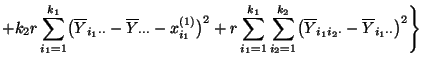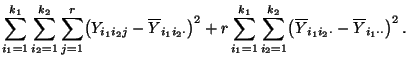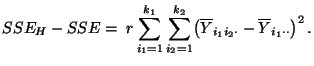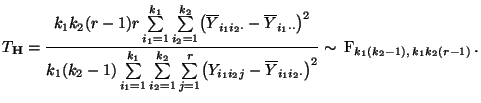Next: Dreifaktorielle Varianzanalyse
Up: Beispiele
Previous: F-Tests für die zweifaktorielle
Contents
Zweifaktorielle Varianzanalyse mit hierarchischer Klassifikation
- Signifikanz des übergeordneten Einflußfaktors
-
- Genauso wie in Abschnitt 4.4.2 läßt sich zunächst
ein Test zur Untersuchung der Frage konstruieren, ob die Stufen
des übergeordneten Einflußfaktors signifikant sind. Hierfür prüfen
wir die Hypothese, ob die gemittelten Effekte
 gleich sind, wobei
gleich sind, wobei
- Mit anderen Worten: Wir testen wir die Hypothese
- Dabei kann man (so wie in Übungsaufgabe 12.3) zeigen, daß die
Nullhypothese die Form
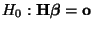 hat, wobei
hat, wobei
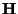 eine
eine
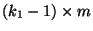 Matrix mit vollem Zeilenrang
Matrix mit vollem Zeilenrang
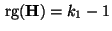 ist und sämtliche Komponenten des Vektors
ist und sämtliche Komponenten des Vektors
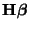 schätzbare Funktionen von
schätzbare Funktionen von
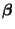 sind.
sind.
- Zur Verifizierung der Hypothese
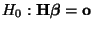 kann
somit die in Theorem 4.14 betrachtete Testgröße
verwendet werden mit
kann
somit die in Theorem 4.14 betrachtete Testgröße
verwendet werden mit
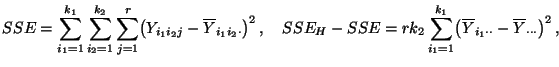 |
(87) |
wobei die Formeln in (87) genauso wie
(82) bzw. (83) bewiesen werden.
- Signifikanz des untergeordneten Einflußfaktors
-
- Um zu prüfen, ob die Stufen des untergeordneten Einflußfaktors
signifikant sind, kann man ähnlich wie bei dem letzten Test in
Abschnitt 4.4.2 (auf Signifikanz der
Wechselwirkungen) vorgehen. Hierfür testen wir die Hypothese
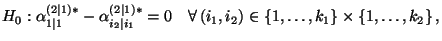 |
(88) |
wobei
- Man kann zeigen, daß sich die in (84) betrachtete
Hypothese in der Form
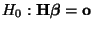 schreiben läßt,
wobei
schreiben läßt,
wobei
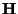 eine
eine
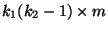 Matrix mit vollem
Zeilenrang
Matrix mit vollem
Zeilenrang
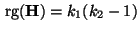 ist und sämtliche Komponenten
des Vektors
ist und sämtliche Komponenten
des Vektors
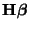 schätzbare Funktionen von
schätzbare Funktionen von
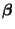 sind.
sind.
- Zur Verifizierung der Hypothese
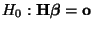 kann
somit die in Theorem 4.14 betrachtete Testgröße
verwendet werden, wobei sich die in (68) bzw.
(69) definierten Quadratsummen
kann
somit die in Theorem 4.14 betrachtete Testgröße
verwendet werden, wobei sich die in (68) bzw.
(69) definierten Quadratsummen 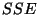 und
und 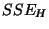 wie folgt bestimmen lassen.
wie folgt bestimmen lassen.
- Und zwar gilt so wie bisher
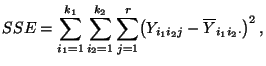 |
(89) |
und die Menge
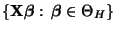 läßt sich
durch die Menge
läßt sich
durch die Menge
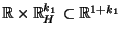 derjenigen Vektoren
derjenigen Vektoren
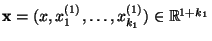 beschreiben, für die
beschreiben, für die
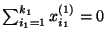 .
.
- Somit ergibt sich, daß
- Hieraus und aus (89) folgt, daß
- Somit gilt




Next: Dreifaktorielle Varianzanalyse
Up: Beispiele
Previous: F-Tests für die zweifaktorielle
Contents
Ursa Pantle
2003-03-10
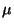 erneut als allgemeines Mittel der Erwartungswerte
erneut als allgemeines Mittel der Erwartungswerte
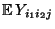 der Stichprobenvariablen
der Stichprobenvariablen
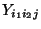 aufgefaßt,
aufgefaßt,
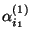 wird Effekt der
wird Effekt der 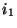 -ten Stufe des
übergeordneten Einflußfaktors genannt, und
-ten Stufe des
übergeordneten Einflußfaktors genannt, und
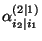 heißt Effekt der
heißt Effekt der
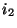 -ten Stufe des untergeordneten Einflußfaktors bei Vorliegen
der
-ten Stufe des untergeordneten Einflußfaktors bei Vorliegen
der 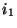 -ten Stufe des übergeordneten Einflußfaktors.
-ten Stufe des übergeordneten Einflußfaktors.