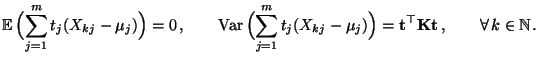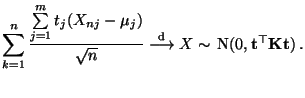Next: Asymptotische Verteilung der Pearson-Statistik
Up: -Anpassungstest von Pearson
Previous: Pearson-Teststatistik
Contents
Multivariater zentraler Grenzwertsatz und weitere
Hilfsmittel
Wir bestimmen die Verteilung der Testgröße 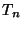 näherungsweise
für große
näherungsweise
für große 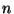 und verwenden hierfür den Begriff der Verteilungskonvergenz von Zufallsvektoren.
und verwenden hierfür den Begriff der Verteilungskonvergenz von Zufallsvektoren.
- Definition
-
Wir benötigen den folgenden Stetigkeitssatz für
charakteristische Funktionen von Zufallsvektoren, der eine
mehrdimensionale Verallgemeinerung von Theorem WR-5.20 ist und den
wir hier ohne Beweis angeben.
Lemma 5.2

Sei
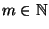
, und seien
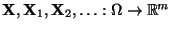
beliebige
Zufallsvektoren. Es gilt
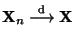
genau dann, wenn
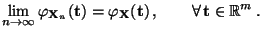 |
(10) |
Außerdem benötigen wir den folgenden
- multivariaten zentralen Grenzwertsatz für Summen von
unabhängigen, identisch verteilten Zufallsvektoren,
- der eine Verallgemeinerung des entsprechenden (1-dimensionalen)
zentralen Grenzwertsatzes für reellwertige Zufallsvariablen ist,
vgl. Theorem WR-5.16.
- Beweis
-
- Wegen Lemma 5.2 ist die Verteilungskonvergenz
(11) äquivalent mit
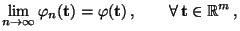 |
(12) |
wobei
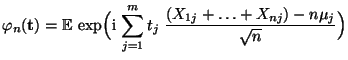 |
(13) |
die charakteristische Funktion von
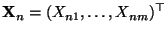 und
und
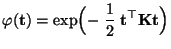 |
(14) |
die charakteristische Funktion der N
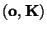 -Verteilung
ist.
-Verteilung
ist.
- Für die in (13) betrachtete charakteristische
Funktion
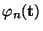 gilt die Darstellungsformel
gilt die Darstellungsformel
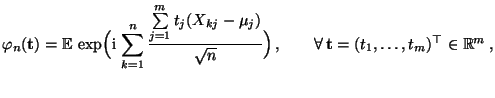 |
(15) |
wobei
- Hieraus folgt, daß die Zahl
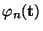 der Wert der
charakteristischen Funktion der reellwertigen Zufallsvariable
der Wert der
charakteristischen Funktion der reellwertigen Zufallsvariable
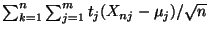 an der
Stelle
an der
Stelle 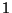 ist.
ist.
- Außerdem ergibt sich aus (14), daß
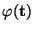 der Wert der charakteristischen Funktion der (1-dimensionalen)
Normalverteilung N
der Wert der charakteristischen Funktion der (1-dimensionalen)
Normalverteilung N
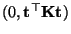 an der Stelle
an der Stelle 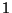 ist.
ist.
- Andererseits ergibt sich aus Theorem WR-5.16, d.h., aus dem
(1-dimensionalen) zentralen Grenzwertsatz für reellwertige
Zufallsvariablen, daß für
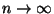
- Hieraus, aus (14) - (15) und aus
Theorem WR-5.20, d.h., aus dem Stetigkeitssatz für
charakteristische Funktionen von reellwertigen Zufsllsvariablen
ergibt sich nun die Gültigkeit von (12).

- Beachte
 Die Idee, den Beweis des multivariaten zentralen Grenzwertsatzes
in Lemma 5.3 mit Hilfe des Stetigkeitssatzes für
charakteristische Funktionen von Zufallsvektoren auf den
zentralen Grenzwertsatz für
reellwertige Zufallsvariablen zurückzuführen, wird in der
englischsprachigen Literatur Cramèr-Wold Device genannt.
Die Idee, den Beweis des multivariaten zentralen Grenzwertsatzes
in Lemma 5.3 mit Hilfe des Stetigkeitssatzes für
charakteristische Funktionen von Zufallsvektoren auf den
zentralen Grenzwertsatz für
reellwertige Zufallsvariablen zurückzuführen, wird in der
englischsprachigen Literatur Cramèr-Wold Device genannt.
Schließlich benötigen wir noch eine vektorielle Version des Continuous Mapping Theorems, das wir in Theorem WR-5.12 für die
Verteilungskonvergenz von stetigen Funktionen reellwertiger
Zufallsvariablen hergeleitet hatten.
Lemma 5.4
- Sei
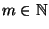 , seien
, seien
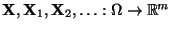 beliebige Zufallsvektoren, und sei
beliebige Zufallsvektoren, und sei
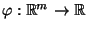 eine
stetige Funktion.
eine
stetige Funktion.
- Dann gilt
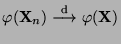 , falls
, falls
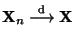 .
.
Der Beweis von Lemma 5.4 verläuft ähnlich wie
der Beweis von Theorem WR-5.12 und wird deshalb weggelassen.




Next: Asymptotische Verteilung der Pearson-Statistik
Up: -Anpassungstest von Pearson
Previous: Pearson-Teststatistik
Contents
Ursa Pantle
2003-03-10
![]() näherungsweise
für große
näherungsweise
für große ![]() und verwenden hierfür den Begriff der Verteilungskonvergenz von Zufallsvektoren.
und verwenden hierfür den Begriff der Verteilungskonvergenz von Zufallsvektoren.