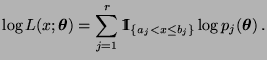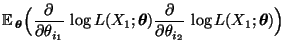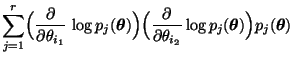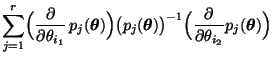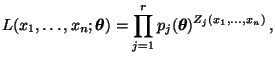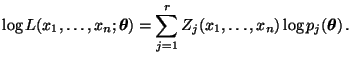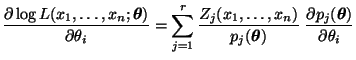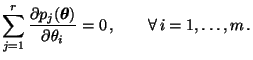Next: Asymptotische Verteilung der Pearson-Fisher-Statistik
Up: -Anpassungstest von Pearson-Fisher
Previous: Pearson-Fisher-Teststatistik
Contents
Asymptotische Normalverteiltheit von Maximum-Likelihood-Schätzern
Ähnlich wie in Abschnitt I.2.4.2, wo der Fall 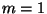 betrachtet
wurde, läßt sich ein multivariater zentraler Grenzwertsatz
für konsistente Folgen von Maximum-Likelihood-Schätzern des
Parametervektors
betrachtet
wurde, läßt sich ein multivariater zentraler Grenzwertsatz
für konsistente Folgen von Maximum-Likelihood-Schätzern des
Parametervektors
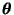 herleiten.
herleiten.
Dabei werden die folgenden Regularitätsbedingungen benötigt.
- Beachte
-
- Zur Erinnerung: Der Begriff des Maximum-Likelihood-Schätzers
wurde bereits in der Vorlesung ,,Statistik I'' eingeführt, vgl.
Abschnitt I.2.2.2. Und zwar
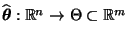 eine
Stichprobenfunktion mit
eine
Stichprobenfunktion mit
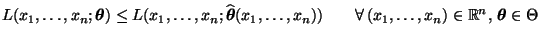 |
(27) |
wobei
- Der Zufallsvektor
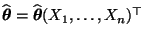 wird
dann Maximum-Likelihood-Schätzer für
wird
dann Maximum-Likelihood-Schätzer für
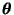 genannt.
genannt.
- Unter den obengenannten Regularitätsbedingungen genügt der
Maximum-Likelihood-Schätzer
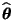 für beliebige
für beliebige
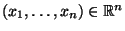 dem Gleichungssystem
dem Gleichungssystem
Um den multivariaten zentralen Grenzwertsatz formulieren zu
können, verallgemeinern wir noch den Begriff der
Fischer-Information, die für 1-dimensionale Parameter bereits in
Abschnitt I.2.3.2 eingeführt wurde.
- Definition
 Für jedes
Für jedes
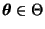 wird die
wird die 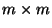 Matrix
Matrix
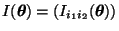 mit
mit
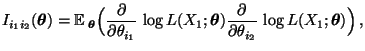 |
(28) |
Fisher-Informationsmatrix genannt, wobei vorausgesetzt wird,
daß der Erwartungswert in (28) für beliebige
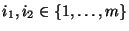 wohldefiniert und endlich ist.
wohldefiniert und endlich ist.
In Verallgemeinerung von Theorem I.2.11, wo der 1-dimensionale
Fall betrachtet wurde, läßt sich sich der folgende multivariate
zentrale Grenzwertsatz für konsistente Folgen von
Maximum-Likelihood-Schätzern des Parametervektors
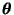 herleiten.
herleiten.
Der Beweis von Theorem 5.2 verläuft ähnlich
wie der Beweis von Theorem I.2.11 und wird deshalb hier
weggelassen, vgl. beispielsweise E.L. Lehmann und G. Casella
(1998) The Theory of Point Estimation, Springer-Verlag, New
York.
Wir kehren nun zu dem ,,vergröberten'' Modell zurück, das in
Abschnitt 5.2.1 betrachtet wurde. Dabei setzen wir
voraus, daß die entsprechende Likelihood-Funktion
![% latex2html id marker 46839
$ L:\mathbb{R}\times\Theta\to[0,1]$](img2321.png) mit
mit
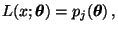 ![$\displaystyle \mbox{falls $x\in(a_j,b_j]$,}$](img2323.png) |
(30) |
die obengenannten Regularitätsbedingungen erfüllt, wobei
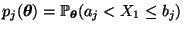 .
.
Lemma 5.5

Für die Fisher-Informationsmatrix
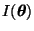
gilt dann
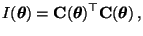 |
(31) |
wobei
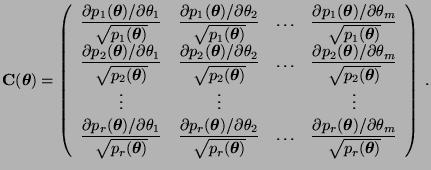 |
(32) |
- Beweis
-
- Für jedes
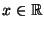 gilt
gilt
- Hieraus ergibt sich für die Eintragungen
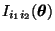 von
von
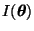 , daß
, daß

- Beachte
-
- Aus (30) ergibt sich für die Likelihood-Funktion
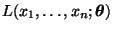 , daß
bzw. für die Loglikelihood-Funktion
, daß
bzw. für die Loglikelihood-Funktion
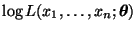 , daß
, daß
- Jede aus den gruppierten Daten
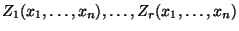 gewonnene
Maximum-Likelihood-Schätzung
gewonnene
Maximum-Likelihood-Schätzung
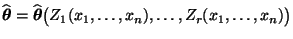 für
für
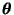 genügt dem Gleichungssystem:
genügt dem Gleichungssystem:
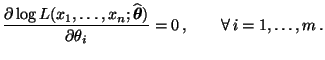 |
(33) |
- Dabei gilt für beliebige
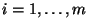 und
und
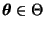 ,
daß
bzw.
,
daß
bzw.
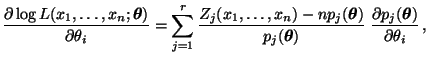 |
(34) |
wobei sich die letzte Gleichheit aus der Tatsache ergibt, daß
Aus Theorem 5.2 ergibt sich somit das
folgende Resultat.
Korollar 5.1

Falls die durch
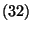
gegebene Matrix
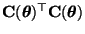
für jedes
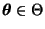
positiv definit
ist, dann gilt
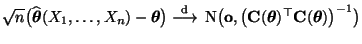 |
(35) |
für jede schwach konsistente Folge
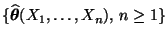
von
Maximum-Likelihood-Schätzern für
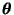
, die durch die
Beobachtung des ,,vergröberten'' Modells gewonnen werden.




Next: Asymptotische Verteilung der Pearson-Fisher-Statistik
Up: -Anpassungstest von Pearson-Fisher
Previous: Pearson-Fisher-Teststatistik
Contents
Ursa Pantle
2003-03-10
![]() betrachtet
wurde, läßt sich ein multivariater zentraler Grenzwertsatz
für konsistente Folgen von Maximum-Likelihood-Schätzern des
Parametervektors
betrachtet
wurde, läßt sich ein multivariater zentraler Grenzwertsatz
für konsistente Folgen von Maximum-Likelihood-Schätzern des
Parametervektors
![]() herleiten.
herleiten.
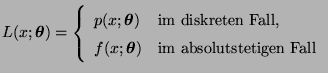
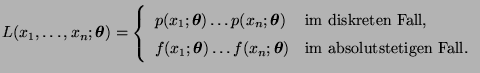
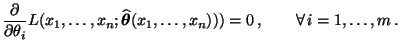
![]() herleiten.
herleiten.
![]() mit
mit