



Next: Asymptotische Normalverteiltheit von Maximum-Likelihood-Schätzern
Up: -Anpassungstest von Pearson-Fisher
Previous: -Anpassungstest von Pearson-Fisher
Contents
Pearson-Fisher-Teststatistik
- So wie in Abschnitt 5.1.1 ,,vergröbern'' wir das
Modell, d.h., wir zerlegen den Wertebereich der Zufallsvariablen
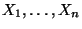 in
in 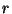 Klassen
Klassen
![$ (a_1,b_1],\ldots,(a_r,b_r]$](img2151.png) mit
wobei
mit
wobei 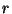 eine (hinreichend große) natürliche Zahl ist.
eine (hinreichend große) natürliche Zahl ist.
- Anstelle des Zufallsvektors
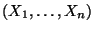 betrachten wir den
Zufallsvektor
betrachten wir den
Zufallsvektor
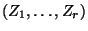 der in bereits in (5)
eingeführten ,,Klassenstärken'', d.h.,
der in bereits in (5)
eingeführten ,,Klassenstärken'', d.h.,
- Gemäß Lemma 5.1 gilt dann
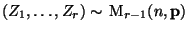 , wobei wir aber nun
annehmen, daß der Parameter
, wobei wir aber nun
annehmen, daß der Parameter
![$ {\mathbf{p}}=(p_1,\ldots,p_{r-1})^\top\in[0,1]^{r-1}$](img2157.png) der
Multinomialverteilung
der
Multinomialverteilung
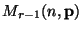 eine (bekannte) Funktion
eine (bekannte) Funktion
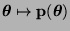 des (unbekannten)
Parametervektors
des (unbekannten)
Parametervektors
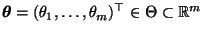 ist, wobei
ist, wobei 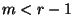 gelte.
gelte.
- Getestet werden soll die Hypothese
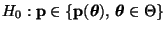 (gegen die
Alternative
(gegen die
Alternative
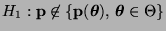 ).
).
- Um bei der Verifizierung dieser Hypothesen ähnlich wie in
Abschnitt 5.1 vorgehen zu können, muß zunächst ein
Schätzer
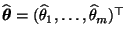 für
für
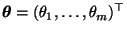 bestimmt werden.
bestimmt werden.
- Damit ist auch gleichzeitig ein Schätzer
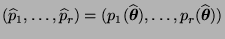 für die
Wahrscheinlichkeiten
für die
Wahrscheinlichkeiten
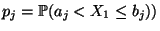 für jedes
für jedes
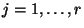 gegeben.
gegeben.
- Definition
 Die Stichprobenfunktion
Die Stichprobenfunktion
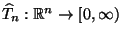 mit
mit
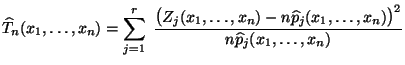 |
(23) |
heißt Pearson-Fisher-Statistik.
- Beachte
-




Next: Asymptotische Normalverteiltheit von Maximum-Likelihood-Schätzern
Up: -Anpassungstest von Pearson-Fisher
Previous: -Anpassungstest von Pearson-Fisher
Contents
Ursa Pantle
2003-03-10