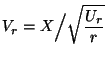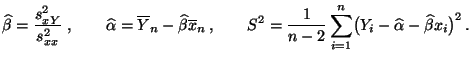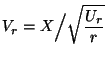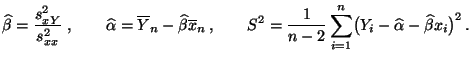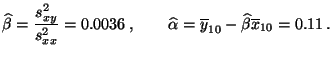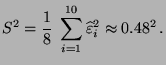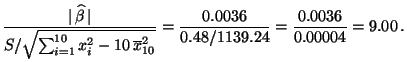Next: Konfidenzintervalle; Prognose von Zielwerten
Up: Einfache lineare Regression
Previous: Normalverteilte Störgrößen
Contents
t-Tests für Regressionskonstante und Regressionskoeffizient
- Für das einfache lineare Regressionsmodell mit normalverteilten
Störgrößen kann man nun t-Tests zur Verifizierung von Hypothesen
über die Regressionskonstante bzw. den Regressionskoeffizienten
mit Hilfe von Theorem 2.5 herleiten, vgl. auch das
Kapitel I.4 über Tests statistischer Hypothesen.
- Zur Erinnerung: Sei
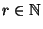 eine beliebige natürliche
Zahl, und seien
eine beliebige natürliche
Zahl, und seien 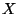 und
und 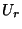 unabhängige Zufallsvariablen mit
unabhängige Zufallsvariablen mit
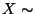 N
N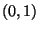 und
und
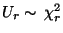 . Dann sagt man (vgl.
Abschnitt I.1.3.4), daß die Zufallsvariable
t-verteilt ist mit
. Dann sagt man (vgl.
Abschnitt I.1.3.4), daß die Zufallsvariable
t-verteilt ist mit 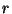 Freiheitsgraden. (Schreibweise:
Freiheitsgraden. (Schreibweise:  t
t )
)
- Die Schätzer
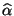 ,
,
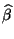 und
und 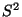 seien so
wie bisher durch (16) bzw. (26)
gegeben, d.h.
seien so
wie bisher durch (16) bzw. (26)
gegeben, d.h.
- Aus den Verteilungs- und Unabhängigkeitseigenschaften, die in
Theorem 2.5 hergeleitet worden sind, ergibt sich nun
unmittelbar, daß
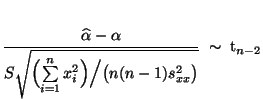 |
(36) |
und
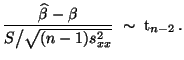 |
(37) |
- Beim Test der Hypothese
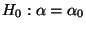 zum Niveau
zum Niveau
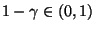 (gegen die Alternative
(gegen die Alternative
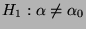 ) wird die Nullhypothese
) wird die Nullhypothese 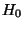 abgelehnt,
falls
abgelehnt,
falls
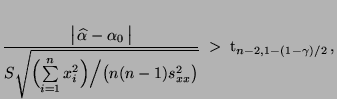 |
(38) |
wobei
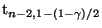 das
das
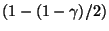 -Quantil der t-Verteilung mit
-Quantil der t-Verteilung mit 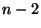 Freiheitsgraden bezeichnet, vgl. Abschnitt I.3.1.2.
Freiheitsgraden bezeichnet, vgl. Abschnitt I.3.1.2.
- Analog wird beim Test der Hypothese
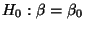 zum Niveau
zum Niveau
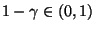 (gegen die Alternative
(gegen die Alternative
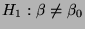 )
die Nullhypothese
)
die Nullhypothese 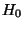 abgelehnt, falls
abgelehnt, falls
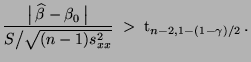 |
(39) |
- Beachte
-
- Beispiel
 (vgl. L.J. Kazmier (1999) Wirtschaftsstatistik.
McGraw-Hill, S. 256ff.)
(vgl. L.J. Kazmier (1999) Wirtschaftsstatistik.
McGraw-Hill, S. 256ff.)




Next: Konfidenzintervalle; Prognose von Zielwerten
Up: Einfache lineare Regression
Previous: Normalverteilte Störgrößen
Contents
Ursa Pantle
2003-03-10