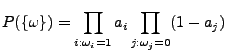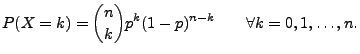Next: Grundlegende Klassen diskreter Verteilungen
Up: Verteilung und Verteilungsfunktion
Previous: Verteilung und Verteilungsfunktion
Contents
Diskrete Zufallsvariablen;
Wahrscheinlichkeitsfunktion
Wir unterscheiden 2 (Grund-) Typen von Zufallsvariablen: diskrete und absolutstetige Zufallsvariablen.
- Definition
 Die Zufallsvariable
Die Zufallsvariable  (bzw. ihre Verteilung)
heißt diskret, falls es eine abzählbare Teilmenge
(bzw. ihre Verteilung)
heißt diskret, falls es eine abzählbare Teilmenge
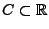 gibt, so dass
gibt, so dass
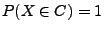 .
.
- Beachte
 Der Begriff der absolutstetigen Zufallsvariablen wird
später in Abschnitt 3.2.4 eingeführt. Wir erwähnen jedoch
schon jetzt ein wichtiges Unterscheidungsmerkmal:
Der Begriff der absolutstetigen Zufallsvariablen wird
später in Abschnitt 3.2.4 eingeführt. Wir erwähnen jedoch
schon jetzt ein wichtiges Unterscheidungsmerkmal:
- diskrete Zufallsvariablen haben einen abzählbaren Wertebereich,
z.B. wenn
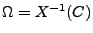 mit
mit
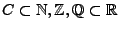 .
Sei beispielsweise
.
Sei beispielsweise 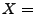 Augensumme bei zweimaligem Würfeln
Augensumme bei zweimaligem Würfeln
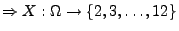
- absolutstetige Zufallsvariablen haben einen überabzählbaren Wertebereich,
z.B.
![$ [a,b],[a,\infty ),(-\infty ,b],\mathbb{R}$](img520.png)
z.B. Roulette mit drehbarem Zeiger und ,,kontinuierlicher'' Skala, wobei
 = Wert des Spiels = Winkel des Zeigers, d.h.
= Wert des Spiels = Winkel des Zeigers, d.h.
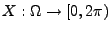
- Definition
 Sei
Sei  eine diskrete Zufallsvariable, d.h., es gebe eine
abzählbare Menge
eine diskrete Zufallsvariable, d.h., es gebe eine
abzählbare Menge
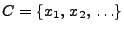 , so dass
, so dass
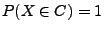 . Dann heißt die Folge
. Dann heißt die Folge
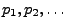 mit
mit
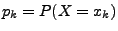 Wahrscheinlichkeitsfunktion
(bzw. Zähldichte) von
Wahrscheinlichkeitsfunktion
(bzw. Zähldichte) von  .
.
- Beachte
-
- Für jede Wahrscheinlichkeitsfunktion
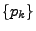 gilt offenbar
gilt offenbar
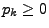 für jedes
für jedes
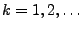 und
und
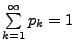 .
.
- Die Verteilung einer diskreten Zufallsvariablen
 wird eindeutig
durch die Wahrscheinlichkeitsfunktion
wird eindeutig
durch die Wahrscheinlichkeitsfunktion
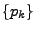 bestimmt, denn es gilt dann für jedes
bestimmt, denn es gilt dann für jedes
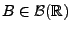
- Für jedes
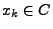 heißt die Zahl
heißt die Zahl
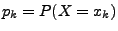 Einzelwahrscheinlichkeit von
Einzelwahrscheinlichkeit von  .
.
- Beispiele
-
- zweimaliges Würfeln
- Bernoulli-Schema
- Einmaliger Münzwurf:
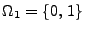 , ,,0'' = Wappen,
,,1'' = Zahl
, ,,0'' = Wappen,
,,1'' = Zahl
 -maliger Münzwurf: Für
-maliger Münzwurf: Für
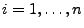 setzen wir
setzen wir
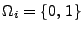 , wobei
, wobei
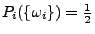 im Fall einer fairen Münze bzw.
allgemein
im Fall einer fairen Münze bzw.
allgemein
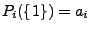 und
und
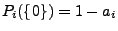 .
.
- Bei identischen Versuchsbedingungen nehmen wir an, dass
![$ a_{1}=a_{2}=\ldots =a_{n}=p,\, p\in [0,\, 1]$](img553.png) .
.
- Unabhängige Versuche modellieren wir durch den Ansatz
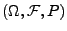 mit
wobei
mit
wobei 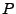 das Produktmaß auf
das Produktmaß auf
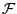 ist, für das gilt:
ist, für das gilt:
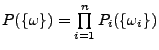 .
.
- Sei
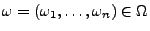 ein
beliebiges Elementarereignis. Dann gilt
ein
beliebiges Elementarereignis. Dann gilt
- Für
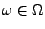 mit
mit
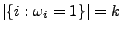 und
und
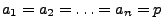 gilt dann insbesondere
gilt dann insbesondere
- Deuten ,,1'' als Erfolg und ,,0'' als Misserfolg.
- Sei
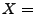 Anzahl der Erfolge bei
Anzahl der Erfolge bei  Versuchen. Falls
Versuchen. Falls
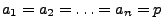 , dann gilt
, dann gilt
- Sprechweise:
 ist binomialverteilt mit den Parametern
ist binomialverteilt mit den Parametern
 und
und 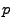 .
.
- Spezialfall: Falls
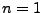 , dann sagen wir, dass
, dann sagen wir, dass  Bernoulli-verteilt ist.
Bernoulli-verteilt ist.




Next: Grundlegende Klassen diskreter Verteilungen
Up: Verteilung und Verteilungsfunktion
Previous: Verteilung und Verteilungsfunktion
Contents
Ursa Pantle
2004-05-10
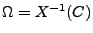 mit
mit
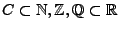 .
Sei beispielsweise
.
Sei beispielsweise 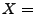 Augensumme bei zweimaligem Würfeln
Augensumme bei zweimaligem Würfeln
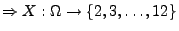
![$ [a,b],[a,\infty ),(-\infty ,b],\mathbb{R}$](img520.png)
 = Wert des Spiels = Winkel des Zeigers, d.h.
= Wert des Spiels = Winkel des Zeigers, d.h.
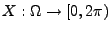
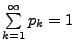 .
.
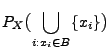
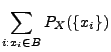
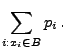
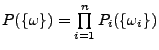 .
.