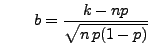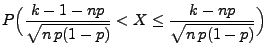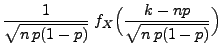Next: Zufallsvektoren
Up: Verteilung und Verteilungsfunktion
Previous: Satz über monotone Klassen
Contents
Verteilungsfunktion;
absolutstetige Zufallsvariablen
Sei
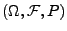 ein beliebiger Wahrscheinlichkeitsraum und
ein beliebiger Wahrscheinlichkeitsraum und
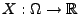 eine beliebige Zufallsvariable.
eine beliebige Zufallsvariable.
- Definition
 Die Funktion
Die Funktion
![$ F_{X}:\mathbb{R}\rightarrow [0,1]$](img607.png) mit
mit
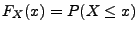 heißt Verteilungsfunktion von
heißt Verteilungsfunktion von  .
.
Wir diskutieren nun zunächst einige Eigenschaften von Verteilungsfunktionen.
Theorem 3.3
Sei
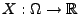
eine beliebige
Zufallsvariable und
![$ F_{X}:\mathbb{R}\rightarrow [0,1]$](img607.png)
ihre
Verteilungsfunktion. Dann gilt
- 1.
- Asymptotisches Verhalten im Unendlichen:
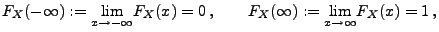 |
(6) |
- 2.
- Monotonie:
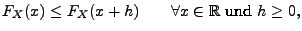 |
(7) |
- 3.
- Rechtsstetigkeit:
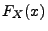 ist rechtsseitig stetig, d.h. für jede Folge
ist rechtsseitig stetig, d.h. für jede Folge
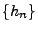 mit
mit
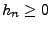 und
und
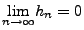 gilt
gilt
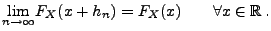 |
(8) |
- Beweis

- Zu 2.
- Weil
![$ (-\infty,x]\subset(-\infty,x+h]$](img616.png) , ergibt sich
aus Teilaussage 2 von Theorem 2.1, dass
, ergibt sich
aus Teilaussage 2 von Theorem 2.1, dass
- Zu 1.
- Wir zeigen nur die erste Teilaussage von
(6). Wegen der Monotonie von
 können wir
o.B.d.A. annehmen, dass
können wir
o.B.d.A. annehmen, dass  monoton gegen
monoton gegen 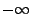 konvergiert. Aus Korollar 2.2 ergibt
sich dann, dass
konvergiert. Aus Korollar 2.2 ergibt
sich dann, dass
Der Beweis der zweiten Teilaussage von (6)
verläuft analog.
- Zu 3.
- Ähnlich wie im Beweis von Teilaussage 1 ergibt sich
aus Korollar 2.2, dass

- Beachte
-
- Mit Hilfe der Verteilungsfunktion
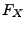 lassen sich auch
die folgenden Wahrscheinlichkeiten ausdrücken
denn es gilt beispielsweise
lassen sich auch
die folgenden Wahrscheinlichkeiten ausdrücken
denn es gilt beispielsweise
- Im allgemeinen gilt jedoch nicht
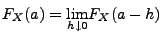 , sondern
, sondern
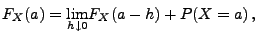 |
(9) |
denn
- In Theorem 3.3 wurde gezeigt,
dass
- Verteilungsfunktionen monotone und beschränkte Funktionen sind.
- Hieraus folgt, dass Verteilungsfunktionen
für jedes
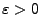 nur endlich viele Sprungstellen
besitzen können, deren Sprunghöhen größer als
nur endlich viele Sprungstellen
besitzen können, deren Sprunghöhen größer als
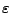 sind.
sind.
- Insgesamt können Verteilungsfunktionen also höchstens
abzählbar viele Sprungstellen besitzen.
- Für die Verteilungsfunktion
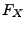 einer diskreten Zufallsvariablen
einer diskreten Zufallsvariablen
 gilt für jedes
gilt für jedes
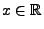 :
:
wobei
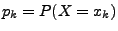 .
.
- Die Verteilungsfunktion
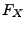 einer diskreten
Zufallsvariablen
einer diskreten
Zufallsvariablen  ist eine sogenannte Treppenfunktion, d.h. eine stückweise konstante Funktion
mit der Sprunghöhe
ist eine sogenannte Treppenfunktion, d.h. eine stückweise konstante Funktion
mit der Sprunghöhe 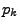 im Punkt
im Punkt 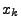 .
.
Theorem 3.4
Sei
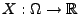
eine beliebige
Zufallsvariable. Dann wird die Verteilung
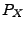
von

durch die
Verteilungsfunktion
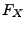
von

eindeutig bestimmt.
- Beweis

- Definition
 Die Zufallsvariable
Die Zufallsvariable
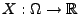 (bzw. ihre Verteilung) heißt absolutstetig,
falls die Verteilungsfunktion
(bzw. ihre Verteilung) heißt absolutstetig,
falls die Verteilungsfunktion 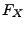 von
von  die folgende
Integraldarstellung
die folgende
Integraldarstellung
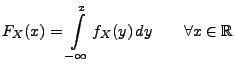 |
(12) |
besitzt, wobei
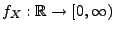 eine (Lebesgue-integrierbare)
Funktion mit nichtnegativen Werten ist, die Dichte (bzw. Wahrscheinlichkeitsdichte) von
eine (Lebesgue-integrierbare)
Funktion mit nichtnegativen Werten ist, die Dichte (bzw. Wahrscheinlichkeitsdichte) von  genannt wird. Das
Integral in (12) wird im allgemeinen als Lebesgue-Integral
aufgefasst.
genannt wird. Das
Integral in (12) wird im allgemeinen als Lebesgue-Integral
aufgefasst.
Die Verteilungsfunktion 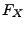 (und damit auch die Verteilung
(und damit auch die Verteilung
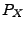 ) einer absolutstetigen Zufallsvariablen
) einer absolutstetigen Zufallsvariablen  wird in dem
folgenden Sinne eindeutig durch die Dichte
wird in dem
folgenden Sinne eindeutig durch die Dichte 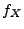 bestimmt.
bestimmt.
- Beweis
-
- Die Hinlänglichkeit der Bedingung (13) ist
offensichtlich, denn es genügt, in (13) die
spezielle Borel-Menge
![$ B=(-\infty,x]$](img466.png) einzusetzen, um
(12) zu erhalten.
einzusetzen, um
(12) zu erhalten.
- Die Notwendigkeit der Bedingung (13) ergibt sich
aus (12) und aus dem eineindeutigen Zusammenhang
zwischen Verteilung und Verteilungsfunktion, vgl.
Theorem 3.4.
- Die Notwendigkeit und Hinlänglichkeit von Bedingung
(14) ergibt sich aus den allgemeinen
(Eindeutigkeits-) Eigenschaften von Lebesgue-Integralen, vgl.
die Vorlesung Analysis III.

- Beachte
-
- Bei vielen Anwendungen ist die Dichte
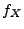 eine (zumindest
stückweise) stetige Funktion. Das Integral in der
Definitionsgleichung (12) ist dann ein
uneigentliches Riemann-Integral.
eine (zumindest
stückweise) stetige Funktion. Das Integral in der
Definitionsgleichung (12) ist dann ein
uneigentliches Riemann-Integral.
- Falls
 absolutstetig ist, dann hat die
Verteilungsfunktion
absolutstetig ist, dann hat die
Verteilungsfunktion 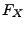 keine Sprünge, d.h.,
keine Sprünge, d.h., 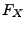 ist eine
(im üblichen Sinne) stetige Funktion. Hieraus und aus
(9) folgt insbesondere, dass
ist eine
(im üblichen Sinne) stetige Funktion. Hieraus und aus
(9) folgt insbesondere, dass
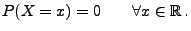 |
(15) |
- Die Verteilungsfunktion
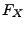 einer absolutstetigen
Zufallsvariablen
einer absolutstetigen
Zufallsvariablen  ist jedoch im allgemeinen nicht
überall differenzierbar. Und zwar ist
ist jedoch im allgemeinen nicht
überall differenzierbar. Und zwar ist 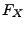 dort nicht
differenzierbar, wo die Dichte
dort nicht
differenzierbar, wo die Dichte 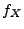 Sprungstellen hat.
Sprungstellen hat.
- Beispiele
 Um die Verteilung einer absolutstetigen
Zufallsvariablen
Um die Verteilung einer absolutstetigen
Zufallsvariablen  zu beschreiben,
genügt es, die Dichte
zu beschreiben,
genügt es, die Dichte 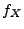 zu betrachten, weil durch
zu betrachten, weil durch 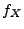 die
Verteilungsfunktion
die
Verteilungsfunktion 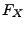 und damit auch die Verteilung
und damit auch die Verteilung 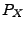 von
von  eindeutig bestimmt wird.
eindeutig bestimmt wird.
- Normalverteilung N
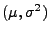 mit den
Parametern
mit den
Parametern
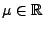 und
und
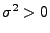 :
:
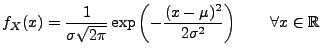 |
(16) |
Spezialfall: Standardnormalverteilung N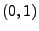 . Dann
nimmt die Dichte
. Dann
nimmt die Dichte 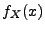 in (16) die folgende Form
an:
in (16) die folgende Form
an:
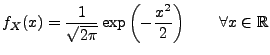 |
(17) |
- Exponentialverteilung Exp
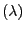 mit Parameter
mit Parameter
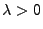 :
:
- Gleichverteilung U
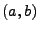 mit den Parametern
mit den Parametern
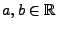 , wobei
, wobei 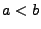 :
:
- Beachte
-
- Absolutstetige Verteilungen treten oft als
(asymptotische) Näherungslösungen auf.
- So lässt sich beispielsweise die Binomialverteilung mit den
Parametern
 und
und 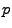 durch die Standardnormalverteilung
approximieren, falls
durch die Standardnormalverteilung
approximieren, falls  groß ist. Dies ist
der folgende zentrale Grenzwertsatz von
DeMoivre-Laplace.
groß ist. Dies ist
der folgende zentrale Grenzwertsatz von
DeMoivre-Laplace.
Theorem 3.6
Für beliebige
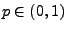
und
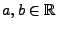
mit
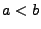
gilt
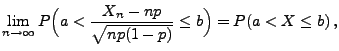 |
(18) |
wobei
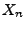
binomialverteilt (mit den Parametern

und
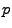
) und

standardnormalverteilt ist.
Der Beweis von Theorem 3.6 wird zunächst weggelassen und
später, in Abschnitt 5.3 der Vorlesung, in einem allgemeineren
Zusammenhang nachgeholt.
- Beachte
-




Next: Zufallsvektoren
Up: Verteilung und Verteilungsfunktion
Previous: Satz über monotone Klassen
Contents
Ursa Pantle
2004-05-10
![]() ein beliebiger Wahrscheinlichkeitsraum und
ein beliebiger Wahrscheinlichkeitsraum und
![]() eine beliebige Zufallsvariable.
eine beliebige Zufallsvariable.
![$\displaystyle P_X\bigl(\bigcap\limits_{x\le 0}(-\infty,x]\bigr)$](img622.png)
![$\displaystyle P_X\bigl(\bigcap\limits_{n\ge 1}(-\infty,x+h_n]\bigr)$](img626.png)
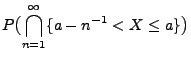
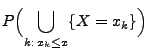
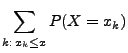
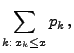
![]() (und damit auch die Verteilung
(und damit auch die Verteilung
![]() ) einer absolutstetigen Zufallsvariablen
) einer absolutstetigen Zufallsvariablen ![]() wird in dem
folgenden Sinne eindeutig durch die Dichte
wird in dem
folgenden Sinne eindeutig durch die Dichte ![]() bestimmt.
bestimmt.
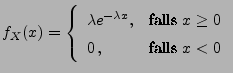
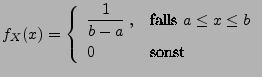
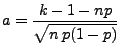 und
und