Unabhängigkeit zusammengesetzter Abbildungen

Das folgende Resultat ist eine sehr nützliche Eigenschaft von unabhängigen Zufallsvariablen.

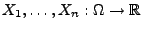
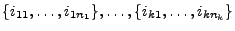
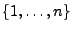
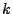
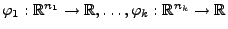
Theorem 3.18   Seien $X_1,\ldots,X_n:\Omega\to\mathbb{R}$ unabhängige Zufallsvariable, und $\{i_{11},\ldots,i_{1n_1}\},\ldots,\{i_{k1},\ldots,i_{kn_k}\}$ sei eine beliebige Zerlegung der Menge $\{1,\ldots,n\}$ in $k$ nichtleere, paarweise disjunkte Teilmengen. Für beliebige Borel-messbare Funktionen $\varphi_1:\mathbb{R}^{n_1}\to\mathbb{R},\ldots,\varphi_k:\mathbb{R}^{n_k}\to\mathbb{R}$ sind dann auch

$$\varphi_1(X_{i_{11}},\ldots,X_{i_{1n_1}}),\ldots, \varphi_k(X_{i_{k1}},\ldots,X_{i_{kn_k}})$$

unabhängige Zufallsvariablen.

Beweis

 

• Wegen der Unabhängigkeit der Zufallsvariablen $X_1,\ldots,X_n:\Omega\to\mathbb{R}$ ergibt sich aus Formel (28) in Theorem 3.10, dass
  

  $${ P((X_{i_{11}},\ldots,X_{i_{1n_1}})\in B_{i_{11}}\times\ldots\ti... ...(X_{i_{k1}},\ldots,X_{i_{kn_k}})\in B_{i_{k1}}\times\ldots\times B_{i_{kn_k}})}$$

  $$= P((X_{i_{11}},\ldots,X_{i_{1n_1}})\in B_{i_{11}}\times\ldots\time... ...((X_{i_{k1}},\ldots,X_{i_{kn_k}})\in B_{i_{k1}}\times\ldots\times B_{i_{kn_k}})$$

  
  
  für beliebige $B_1,\ldots,B_n\in\mathcal{B}(\mathbb{R})$.
• Sei $\mathcal{G}$ das $\pi$-System $\mathcal{G}=\{B_1\times\ldots\times B_{n_1},\,B_1,\ldots, B_{n_1}\in\mathcal{B}(\mathbb{R})\}$, und sei $\mathcal{D}$ das $d$-System derjenigen Borel-Mengen $C_1\in\mathcal{B}(\mathbb{R}^{n_1})$, für die gilt
  

  $${ P((X_{i_{11}},\ldots,X_{i_{1n_1}})\in C_1,(X_{i_{21}},\ldots,X_{i_{2n_2}})\in B_{i_{21}}\times\ldots\times B_{i_{2n_2}},}$$

  $$\hspace{4cm} \ldots, (X_{i_{k1}},\ldots,X_{i_{kn_k}})\in B_{i_{k1}}\times\ldots\times B_{i_{kn_k}})$$

  $$= P((X_{i_{11}},\ldots,X_{i_{1n_1}})\in C_1)\,P((X_{i_{21}},\ldots,X_{i_{2n_2}})\in B_{i_{21}}\times\ldots\times B_{i_{2n_2}})$$

  $$\hspace{4cm} \ldots P( (X_{i_{k1}},\ldots,X_{i_{kn_k}})\in B_{i_{k1}}\times\ldots\times B_{i_{kn_k}})\,.$$

  
  

• Dann ergibt sich mit Hilfe des Satzes über monotone Klassen (vgl. Theorem 3.2), dass
  $$\mathcal{D}\supset d(\mathcal{G})=\sigma(\mathcal{G})=\mathcal{B}(\mathbb{R}^{n_1})\,.$$

• Hieraus und durch wiederholte Anwendung des Satzes über monotone Klassen ergibt sich also, dass
  

  $${ P((X_{i_{11}},\ldots,X_{i_{1n_1}})\in C_1,\ldots, (X_{i_{k1}},\ldots,X_{i_{kn_k}})\in C_k)}$$

  $$= P\bigl((X_{i_{11}},\ldots,X_{i_{1n_1}})\in C_1\bigr)\ldots P\bigl((X_{i_{k1}},\ldots,X_{i_{kn_k}})\in C_k\bigr)$$ (50)

  
  
  für beliebige $C_1\in\mathcal{B}(\mathbb{R}^{n_1}),\ldots,C_k\in\mathcal{B}(\mathbb{R}^{n_k})$.
• Somit gilt für beliebige Borel-Mengen $B_1,\ldots,B_k\in\mathcal{B}(\mathbb{R})$, dass
  

  $${P(\varphi_1(X_{i_{11}},\ldots,X_{i_{1n_1}})\in B_1,\ldots, \varphi_k(X_{i_{k1}},\ldots,X_{i_{kn_k}})\in B_k)}$$

  $$= P((X_{i_{11}},\ldots,X_{i_{1n_1}})\in \varphi_1^{-1}(B_1),\ldots, (X_{i_{k1}},\ldots,X_{i_{kn_k}})\in \varphi_k^{-1}(B_k))$$

  $$= P\bigl((X_{i_{11}},\ldots,X_{i_{1n_1}})\in \varphi_1^{-1}(B_1)\bigr)\ldots P\bigl((X_{i_{k1}},\ldots,X_{i_{kn_k}})\in \varphi_k^{-1}(B_k)\bigr)$$

  $$= P(\varphi_1(X_{i_{11}},\ldots,X_{i_{1n_1}})\in B_1)\ldots P(\varphi_k(X_{i_{k1}},\ldots,X_{i_{kn_k}})\in B_k)\,,$$

  
  

• wobei sich die vorletzte Gleichheit aus (50) ergibt mit $C_i=\varphi_i^{-1}(B_i)$.
• Durch die erneute Anwendung von Theorem 3.10 erhalten wir nun die Behauptung.
  
  $\Box$