- Eine Familie
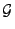 von Teilmengen von
von Teilmengen von  heißt
heißt
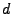 -System auf
-System auf  , falls
, falls
-
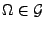 ,
,
-
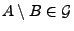 für beliebige
für beliebige
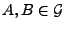 mit
mit
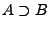 ,
,
-
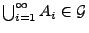 für beliebige
für beliebige
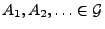 mit
mit
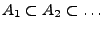 .
.
-
- Eine nichtleere Familie
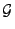 von Teilmengen von
von Teilmengen von  heißt
heißt
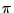 -System auf
-System auf  , falls
, falls
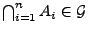 für jedes
für jedes
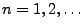 und für beliebige
und für beliebige
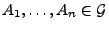 .
.
- Jede
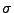 -Algebra auf
-Algebra auf  ist gleichzeitig ein
ist gleichzeitig ein 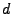 -System
und auch ein
-System
und auch ein 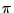 -System auf
-System auf  .
.
- Umgekehrt ist jedes System von Teilmengen von
 , dass
sowohl ein
, dass
sowohl ein 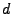 -System als auch ein
-System als auch ein 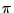 -System auf
-System auf  ist,
eine
ist,
eine 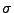 -Algebra auf
-Algebra auf  .
.
- Schreibweise: Sei
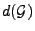 das kleinste
das kleinste 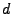 -System, das
das erzeugende System
-System, das
das erzeugende System
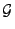 von Teilmengen von
von Teilmengen von  umfasst.
Analog bezeichne
umfasst.
Analog bezeichne
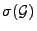 die kleinste
die kleinste 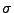 -Algebra,
die das erzeugende System
-Algebra,
die das erzeugende System
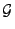 von Teilmengen von
von Teilmengen von  umfasst.
umfasst.