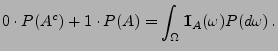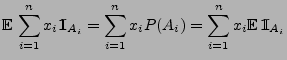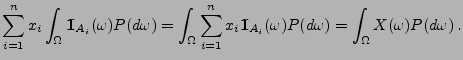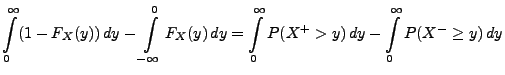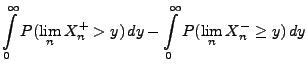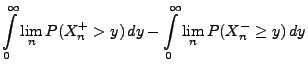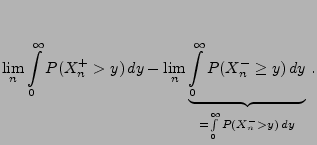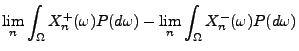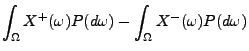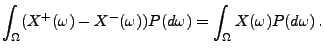Next: Weitere Eigenschaften des Erwartungswertes
Up: Erwartungswert
Previous: Definition und Berechnungsformeln
Contents
Alternative Integral-Darstellungen
Die folgende Darstellungsformel des Erwartungswertes von positiven
Zufallsvariablen ist äußerst nützlich.
Theorem 4.2
Sei
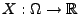
eine beliebige Zufallsvariable mit
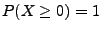
. Dann gilt
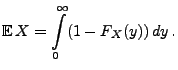 |
(10) |
- Beweis
 Aus der Definitionsgleichung (4) von
Aus der Definitionsgleichung (4) von
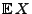 und
aus dem Satz von Fubini ergibt sich, dass
und
aus dem Satz von Fubini ergibt sich, dass

Korollar 4.1
Sei
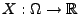
eine integrierbare Zufallsvariable. Dann gilt
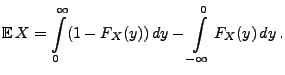 |
(11) |
- Beweis
 Ähnlich wie im Beweis von Theorem 4.2 ergibt sich,
dass
Ähnlich wie im Beweis von Theorem 4.2 ergibt sich,
dass
wobei in der letzten Gleichheit die Formel (10) und
die Tatsache genutzt wird, dass

Wir zeigen nun noch, dass der in (4) definierte
Erwartungswert
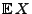 auch in der folgenden Form dargestellt
werden kann.
auch in der folgenden Form dargestellt
werden kann.
Theorem 4.3
Sei
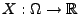
eine beliebige Zufallsvariable, deren
Verteilung der Bedingung
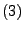
genügt. Dann gilt
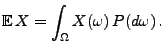 |
(12) |
- Beweis
-
- Wir zeigen die Gültigkeit von (12) zunächst für den
Fall, dass
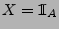 für ein
für ein
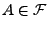 .
.
- Dann gilt
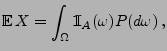 |
(13) |
denn
- Auf analoge Weise lässt sich die Gültigkeit von
(12) für Linearkombinationen von Indikatorvariablen
zeigen.
- Und zwar seien
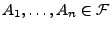 beliebige Ereignisse und
beliebige Ereignisse und
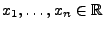 beliebige reelle Zahlen.
beliebige reelle Zahlen.
- Ohne Einschränkung der Allgemeinheit können (und werden) wir
annehmen, dass
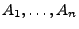 paarweise disjunkte Mengen sind.
paarweise disjunkte Mengen sind.
- Für die Zufallsvariable
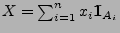 gilt dann
wegen (6) und (13), dass
gilt dann
wegen (6) und (13), dass
- Mit Hilfe des Satzes von Beppo Levi (über die monotone Konvergenz
von Lebesgue-Integralen) wird schließlich gezeigt, dass
(12) für jede Zufallsvariable
 gilt, deren
Verteilung der Bedingung
gilt, deren
Verteilung der Bedingung
 genügt.
genügt.
- Dabei nutzen wir die Tatsache, dass jede Zufallsvariable
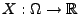 in den positiven Teil
in den positiven Teil
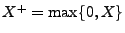 bzw. den
negativen Teil
bzw. den
negativen Teil
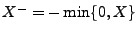 zerlegt werden kann.
zerlegt werden kann.
- Dann gilt
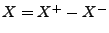 , und es gibt zwei monoton wachsende Folgen
, und es gibt zwei monoton wachsende Folgen
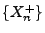 bzw.
bzw. 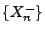 von Linearkombinationen von
Indikatorvariablen, so dass
von Linearkombinationen von
Indikatorvariablen, so dass
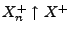 und
und
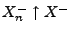 .
.
- Aus Korollar 4.1 und aus dem Satz über die monotone
Konvergenz ergibt sich nun, dass
Durch erneute Anwendung von Korollar 4.1 und des
Satzes über die monotone Konvergenz ergibt sich somit, dass

- Beachte
-
- Die im Beweis von Theorem 4.3 verwendete
Methode wird algebraische Induktion genannt.
- Sie beruht auf dem Prinzip, die betreffende Aussage zunächst
- für Indikatoren von Ereignissen,
- danach für Linearkombinationen von Indikatoren
- und schließlich (durch monotone Approximation und Zerlegung in
Positiv- bzw. Negativteil) für beliebige Zufallsvariablen zu
beweisen.
- Wir werden im folgenden noch weitere Aussagen mit dieser
Beweismethode herleiten.




Next: Weitere Eigenschaften des Erwartungswertes
Up: Erwartungswert
Previous: Definition und Berechnungsformeln
Contents
Ursa Pantle
2004-05-10
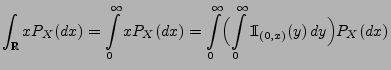
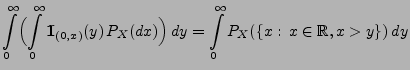
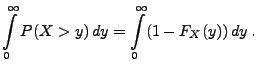
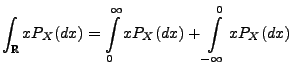
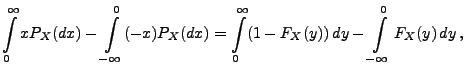
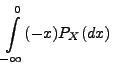
![$\displaystyle \int\limits_{-\infty}^0
\Bigl(\int\limits_0^\infty {1\hspace{-1mm...
...int\limits_{-\infty}^0
{1\hspace{-1mm}{\rm I}}_{(0,-x]}(y)\, P_X(dx)\Bigr)\, dy$](img1116.png)
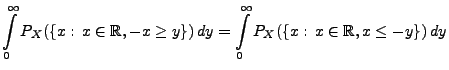
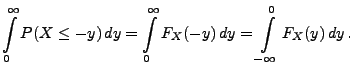
![]() auch in der folgenden Form dargestellt
werden kann.
auch in der folgenden Form dargestellt
werden kann.