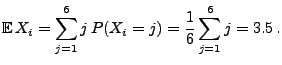- 1.
- Monotonie:
 Falls
Falls  und
und 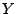 integrierbar sind und falls
integrierbar sind und falls 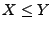 f.s., dann
gilt
f.s., dann
gilt
Falls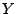 integrierbar ist und falls
integrierbar ist und falls
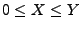 f.s., dann ist
auch
f.s., dann ist
auch  integrierbar, und es gilt
integrierbar, und es gilt
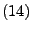 .
.
- 2.
- Falls
 integrierbar ist, dann ist
integrierbar ist, dann ist
- 3.
- Linearität:
 Falls
Falls  und
und 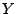 integrierbar sind, dann ist auch
integrierbar sind, dann ist auch 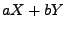 integrierbar für beliebige
integrierbar für beliebige
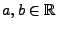 , und es gilt
, und es gilt
- 4.
- monotone Konvergenz:
 Falls
Falls 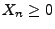 f.s. für alle
f.s. für alle
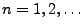 und falls
und falls
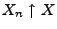 f.s., dann gilt
f.s., dann gilt
- 5.
- majorisierte Konvergenz und
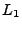 -Konvergenz:
-Konvergenz: Falls
Falls 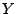 integrierbar ist, falls
integrierbar ist, falls
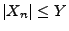 f.s. für alle
f.s. für alle
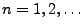 und falls
und falls 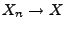 f.s., dann ist auch
f.s., dann ist auch  integrierbar, und es gilt
integrierbar, und es gilt
und
- 6.
 Falls
Falls
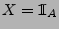 für ein
für ein
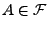 , dann gilt
, dann gilt
- 7.
 Falls
Falls  integrierbar ist und falls
integrierbar ist und falls 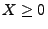 f.s. und
f.s. und
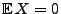 ,
dann gilt
,
dann gilt