- Es ist klar, dass der in (4) definierte
Erwartungswert
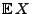 eindeutig durch die Verteilung
eindeutig durch die Verteilung 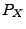 der
Zufallsvariablen
der
Zufallsvariablen  bestimmt wird.
bestimmt wird.
- In Theorem 4.1 hatten wir darüber hinaus gezeigt,
dass der Erwartungswert
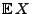 einer diskreten bzw.
absolutstetigen Zufallsvariablen
einer diskreten bzw.
absolutstetigen Zufallsvariablen  eindeutig durch die
Wahrscheinlichkeitsfunktion bzw. die Dichte von
eindeutig durch die
Wahrscheinlichkeitsfunktion bzw. die Dichte von  bestimmt wird.
bestimmt wird.
- Umgekehrt ist jedoch im allgemeinen die Verteilung
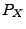 nicht eindeutig durch den Erwartungswert
nicht eindeutig durch den Erwartungswert
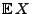 von
von  festgelegt.
festgelegt.
- Insbesondere ist die Wahrscheinlichkeitsfunktion bzw. die Dichte
einer diskreten bzw. absolutstetigen Zufallsvariablen
 nicht
eindeutig durch den Erwartungswert
nicht
eindeutig durch den Erwartungswert
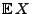 von
von  festgelegt.
festgelegt.
- Sei
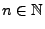 eine beliebige natürliche Zahl und
eine beliebige natürliche Zahl und
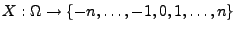 eine diskrete Zufallsvariable
mit
eine diskrete Zufallsvariable
mit
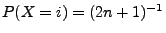 für jedes
für jedes
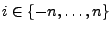 .
.
- Dann gilt
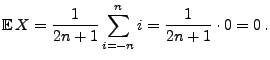
- Während der Erwartungswert
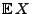 also nicht von
also nicht von  abhängt, sind die Werte von
abhängt, sind die Werte von  mit wachsendem
mit wachsendem  immer
breiter um
immer
breiter um
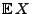 gestreut.
gestreut.
- Eine Charakteristik, die den Streuungsgrad der Werte
von
 um den Erwartungswert
um den Erwartungswert
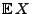 misst, ist die erwartete
quadratische Abweichung
misst, ist die erwartete
quadratische Abweichung
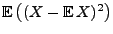 vom Erwartungswert
vom Erwartungswert
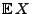 , genannt Varianz von
, genannt Varianz von  ,
die bei diesem Beispiel gegeben ist durch
,
die bei diesem Beispiel gegeben ist durch
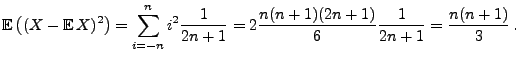
- Der Erwartungswert
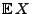 der Zufallsvariablen
der Zufallsvariablen  wird manchmal
auch das erste Moment von
wird manchmal
auch das erste Moment von  genannt.
genannt.
- Völlig analog lassen sich die Begriffe der Varianz bzw. der
höheren Momente einer beliebigen Zufallsvariable
 einführen,
einführen,
- und zwar durch die Betrachtung des Erwartungswertes
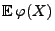 entsprechend gewählter Funktionen
entsprechend gewählter Funktionen
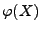 von
von
 .
.
- Sei
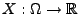 eine beliebige Zufallsvariable mit
eine beliebige Zufallsvariable mit
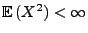 .
.
- Betrachten die Abbildung
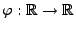 mit
mit
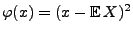 .
.
- Dann heißt der Erwartungswert
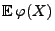 der
Zufallsvariablen
der
Zufallsvariablen
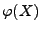 die Varianz von
die Varianz von 
(Schreibweise: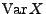 ).
).
- Für die Varianz von
 gilt also
gilt also
- Die höheren Momente von Zufallsvariablen werden völlig analog definiert.
- Und zwar sei
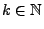 und
und
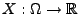 eine beliebige
Zufallsvariable mit
eine beliebige
Zufallsvariable mit
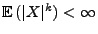 .
.
- Betrachten die Abbildung
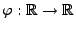 mit
mit
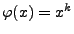 . Dann heißt der Erwartungswert
. Dann heißt der Erwartungswert
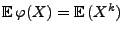 von
von
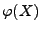 das
das
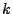 -te Moment von
-te Moment von  .
.
- Betrachten die Abbildung
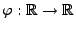 mit
mit
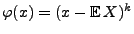 . Dann heißt der Erwartungswert
. Dann heißt der Erwartungswert
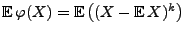 von
von
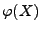 das
das
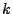 -te zentrale Moment von
-te zentrale Moment von  .
.
- Die Varianz
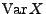 ist also das 2. zentrale Moment von
ist also das 2. zentrale Moment von
 .
.
-
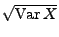 heißt Standardabweichung
von
heißt Standardabweichung
von  .
.