



Next: Ungleichungen für Momente und
Up: Gemischte Momente
Previous: Linearer Zusammenhang von Zufallsvariablen
Contents
Erwartungswertvektor und Kovarianzmatrix
Wir zeigen zunächst, wie der Begriff der Kovarianz genutzt werden
kann, um die in Theorem 4.10 angegebene
Additionsformel (41) für die Varianz zu
verallgemeinern.
Theorem 4.13
Seien
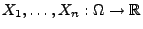
beliebige Zufallsvariablen mit
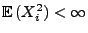
für
jedes
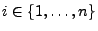
.
- 1.
 Dann gilt
Dann gilt
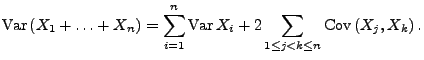 |
(53) |
- 2.
 Falls die Zufallsvariablen
Falls die Zufallsvariablen
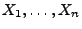 paarweise
unkorreliert sind, dann gilt insbesondere
paarweise
unkorreliert sind, dann gilt insbesondere
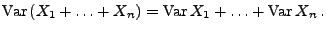 |
(54) |
- Beweis
-
- Wir betrachten zunächst den Fall
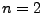 .
.
- Dann ergibt sich sofort aus dem Beweis von
Theorem 4.10, dass
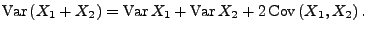 |
(55) |
- Für beliebiges
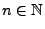 ergibt sich die Gültigkeit
von (53) nun mittels vollständiger
Induktion.
ergibt sich die Gültigkeit
von (53) nun mittels vollständiger
Induktion.
- Und zwar erhalten wir aus (55) und aus
der Induktionsannahme, dass
- Die Gleichung (54) ergibt sich
unmittelbar aus (50) und
(53).

- Beachte
 Neben den Erwartungswerten
Neben den Erwartungswerten
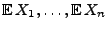 und den Varianzen
und den Varianzen
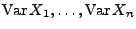 sind die in
(53) auftretenden Kovarianzen
sind die in
(53) auftretenden Kovarianzen
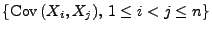 wichtige Charakteristiken des Zufallsvektors
wichtige Charakteristiken des Zufallsvektors
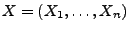 .
.
Dies führt zu den folgenden Begriffsbildungen.
- Definition
 Seien
Seien
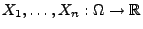 beliebige Zufallsvariablen mit
beliebige Zufallsvariablen mit
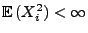 für
jedes
für
jedes
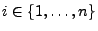 .
.
- Der Vektor
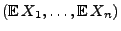 heißt
der Erwartungswertvektor des Zufallsvektors
heißt
der Erwartungswertvektor des Zufallsvektors
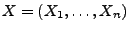 .
.
Schreibweise:
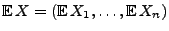
- Die
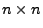 -Matrix
heißt die Kovarianzmatrix von
-Matrix
heißt die Kovarianzmatrix von
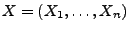 .
.
Theorem 4.14
Die Kovarianzmatrix
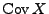
ist
- 1.
- symmetrisch, d.h., für beliebige
 gilt
gilt
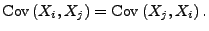 |
(56) |
- 2.
- nichtnegativ definit, d.h., für jedes
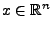 gilt
gilt
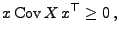 |
(57) |
wobei 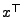 der zu
der zu 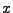 transponierte
Vektor ist.
transponierte
Vektor ist.
- Beweis
-
- Die Symmetrieeigenschaft (56) ergibt
sich unmittelbar aus der
Definitionsgleichung (42)
der Kovarianz.
- Außerdem gilt
- Damit ist auch die Ungleichung (57) bewiesen.

- Beachte
 Die Matrix
Die Matrix
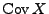 heißt positiv
definit, falls
heißt positiv
definit, falls
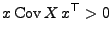 |
(58) |
für jedes
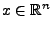 mit
mit 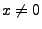 .
.
- Beispiel
 (zweidimensionale Normalverteilung)
(zweidimensionale Normalverteilung)
- Beachte
-
- Die Verteilung eines normalverteilten Zufallsvektors
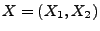 wird eindeutig durch den
Erwartungswertvektor
wird eindeutig durch den
Erwartungswertvektor
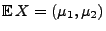 und die
Kovarianzmatrix
und die
Kovarianzmatrix
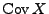 bestimmt.
Für beliebige (nicht normalverteilte)
Zufallsvektoren gilt diese Eindeutigkeitsaussage jedoch im
allgemeinen nicht.
bestimmt.
Für beliebige (nicht normalverteilte)
Zufallsvektoren gilt diese Eindeutigkeitsaussage jedoch im
allgemeinen nicht.
- Es gilt
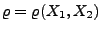 .
Außerdem ergibt sich aus (59), dass
.
Außerdem ergibt sich aus (59), dass
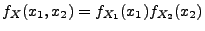 genau dann, wenn
genau dann, wenn 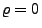 . Die Komponenten
. Die Komponenten 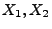 eines
normalverteilten Zufallsvektors
eines
normalverteilten Zufallsvektors
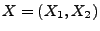 sind also
genau dann unabhängig, wenn sie unkorreliert sind.
sind also
genau dann unabhängig, wenn sie unkorreliert sind.
- Weil
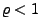 vorausgesetzt wird, ist die
Determinante der Kovarianzmatrix
vorausgesetzt wird, ist die
Determinante der Kovarianzmatrix
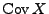 nicht Null,
d.h., die Matrix
nicht Null,
d.h., die Matrix
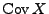 ist positiv definit und invertierbar.
Man kann sich deshalb leicht überlegen, dass die in (59)
gegebenen Dichte
ist positiv definit und invertierbar.
Man kann sich deshalb leicht überlegen, dass die in (59)
gegebenen Dichte 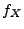 von
von  auch wie folgt dargestellt werden
kann: Es gilt
auch wie folgt dargestellt werden
kann: Es gilt
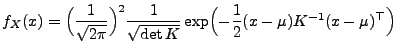 |
(61) |
für jedes
 , wobei
, wobei
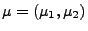 und
und 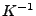 die inverse Matrix zu der in (60) gegebenen
Kovarianzmatrix
die inverse Matrix zu der in (60) gegebenen
Kovarianzmatrix
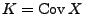 bezeichnet.
bezeichnet.
Schreibweise: 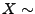 N
N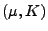 .
.
- Man kann sich leicht überlegen, dass die
Randverteilungen von
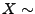 N
N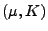 (eindimensionale)
Normalverteilungen sind mit
(eindimensionale)
Normalverteilungen sind mit 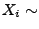 N
N
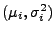 für
für 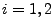 .
.
- Manchmal betrachtet man auch Zufallsvektoren
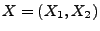 , deren Komponenten
, deren Komponenten 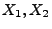 normalverteilt
sind mit
normalverteilt
sind mit
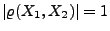 . Aus Theorem 4.12 folgt
dann, dass
. Aus Theorem 4.12 folgt
dann, dass
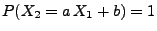 für ein Zahlenpaar
für ein Zahlenpaar
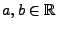 .
In diesem Fall ist der Zufallsvektor
.
In diesem Fall ist der Zufallsvektor
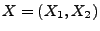 nicht absolutstetig, obwohl seine Komponenten diese
Eigenschaft besitzen.
nicht absolutstetig, obwohl seine Komponenten diese
Eigenschaft besitzen.
Für Zufallsvektoren mit einer beliebigen Dimension
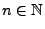 kann man
den Begriff der
kann man
den Begriff der  -dimensionalen Normalverteilung einführen, indem
man eine zu
(61) analoge Dichte-Formel betrachtet.
-dimensionalen Normalverteilung einführen, indem
man eine zu
(61) analoge Dichte-Formel betrachtet.
- Definition
-




Next: Ungleichungen für Momente und
Up: Gemischte Momente
Previous: Linearer Zusammenhang von Zufallsvariablen
Contents
Ursa Pantle
2004-05-10
 Dann gilt
Dann gilt
 Falls die Zufallsvariablen
Falls die Zufallsvariablen
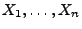 paarweise
unkorreliert sind, dann gilt insbesondere
paarweise
unkorreliert sind, dann gilt insbesondere
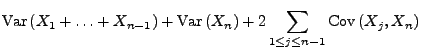
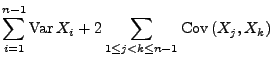
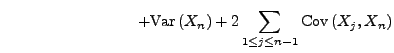
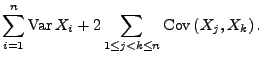
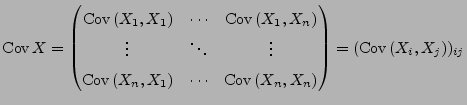
![]() kann man
den Begriff der
kann man
den Begriff der ![]() -dimensionalen Normalverteilung einführen, indem
man eine zu
(61) analoge Dichte-Formel betrachtet.
-dimensionalen Normalverteilung einführen, indem
man eine zu
(61) analoge Dichte-Formel betrachtet.