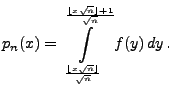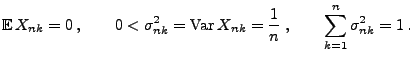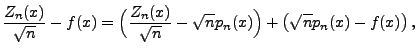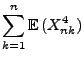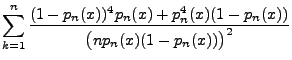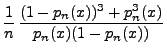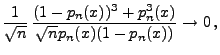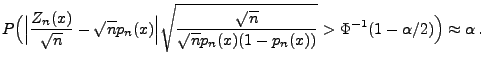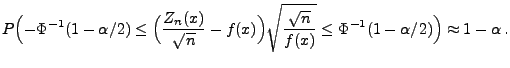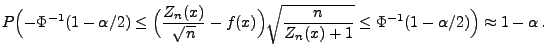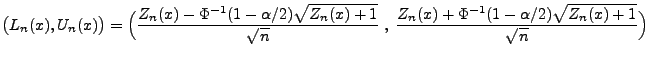Next: Tabellen für Verteilungsfunktionen und
Up: Zentraler Grenzwertsatz
Previous: Bedingungen von Lindeberg und
Contents
Anwendungsbeispiel: Dichteschätzung
- Beachte
 Wegen (115) können wir
Wegen (115) können wir
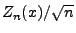 für
hinreichend großes
für
hinreichend großes  als Schätzer des Funktionswertes
als Schätzer des Funktionswertes
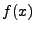 auffassen;
auffassen; 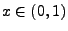 .
.
- Beweis von Theorem 5.25
-
- Die Gültigkeit von (115) ergibt sich aus der
Tschebyschew-Ungleichung (4.72) und aus Satz von
Slutsky (vgl. Theorem 5.9).
- Und zwar sei für beliebige
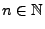 und
und
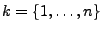
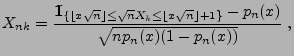 |
(117) |
wobei
- Die so definierten Zufallsvariablen
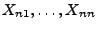 sind
unabhängig und identisch verteilt (wobei ihre Verteilung jedoch
von
sind
unabhängig und identisch verteilt (wobei ihre Verteilung jedoch
von  abhängt), und es gilt
abhängt), und es gilt
- Außerdem gilt die Identität
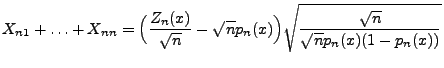 |
(118) |
bzw.
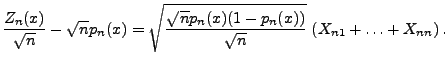 |
(119) |
- Weil
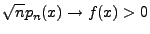 und und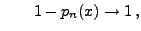 |
(120) |
ergibt sich aus (119) und aus der
Tschebyschew-Ungleichung (4.72), dass
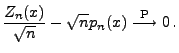 |
(121) |
- Außerdem gilt
- Hieraus und aus (120) - (121) ergibt
sich nun die Gültigkeit von (115) mit Hilfe der
Teilaussage 2 von Theorem 5.8.

- Beachte
 Wenn die Dichte
Wenn die Dichte
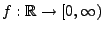 stetig ist, dann kann man mit
Hilfe des zentralen Grenzwertsatzes von Ljapunow (vgl.
Theorem 5.23) ein (zufälliges) Konfidenzintervall konstruieren, in dem der unbekannte
Funktionswert
stetig ist, dann kann man mit
Hilfe des zentralen Grenzwertsatzes von Ljapunow (vgl.
Theorem 5.23) ein (zufälliges) Konfidenzintervall konstruieren, in dem der unbekannte
Funktionswert 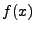 für große
für große  mit einer (näherungsweise
vorgegebenen) ,,großen'' Wahrscheinlichkeit
mit einer (näherungsweise
vorgegebenen) ,,großen'' Wahrscheinlichkeit
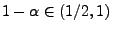 liegt.
liegt.
Theorem 5.26
Die Dichte
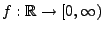
sei stetig, und es gelte
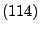
. Dann gilt für jedes
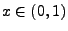
und für
jedes
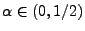
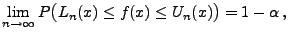 |
(122) |
wobei
und
- Beweis
-
- Aus (120) ergibt sich, dass für
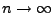
- Die Bedingungen von Theorem 5.23 sind also erfüllt
für
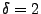 .
.
- Für die in (117) definierten Zufallsvariablen
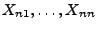 gilt deshalb
gilt deshalb
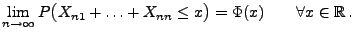 |
(123) |
- Aus der Identität (118) und aus (123)
ergibt sich nun, dass für große

- Wegen (120) ergibt sich hieraus und aus dem Satz von
Slutsky (vgl. Theorem 5.9 bzw. 5.11),
dass
- Auf die gleiche Weise ergibt sich nun hieraus und aus
(115), dass für große

- Durch Umstellen dieser Ungleichungskette nach
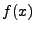 ergibt sich
schließlich das Konfidenzintervall
für den unbekannten Funktionswert
ergibt sich
schließlich das Konfidenzintervall
für den unbekannten Funktionswert 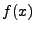 .
.





Next: Tabellen für Verteilungsfunktionen und
Up: Zentraler Grenzwertsatz
Previous: Bedingungen von Lindeberg und
Contents
Ursa Pantle
2004-05-10