



Next: Gesetz der großen Zahlen
Up: Konvergenzarten
Previous: Charakterisierung der Verteilungskonvergenz
Contents
Konvergenz zusammengesetzter
Abbildungen; Satz von Slutsky
Wir zeigen zunächst, dass die fast sichere Konvergenz, die
Konvergenz in Wahrscheinlichkeit, die 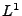 -Konvergenz und die
Konvergenz im quadratischen Mittel bei der Addition von
Zufallsvariablen erhalten bleiben.
-Konvergenz und die
Konvergenz im quadratischen Mittel bei der Addition von
Zufallsvariablen erhalten bleiben.
- Beweis

- Zu 1:
 Falls
Falls
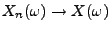 und
und
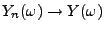 für ein
für ein
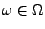 , dann gilt auch
, dann gilt auch
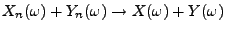 . Hieraus folgt
die erste Teilaussage.
. Hieraus folgt
die erste Teilaussage.
- Zu 2:
 Für jedes
Für jedes
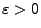 gilt
bzw. nach Übergang zu den Komplementen
Hieraus folgt, dass
und somit die Gültigkeit der zweiten Teilaussage.
gilt
bzw. nach Übergang zu den Komplementen
Hieraus folgt, dass
und somit die Gültigkeit der zweiten Teilaussage.
- Zu 3:
 Die dritte Teilaussage ergibt sich unmittelbar aus der Monotonie
und der Linearität des Erwartungswertes (vgl.
Theorem 4.4), denn es gilt
Die dritte Teilaussage ergibt sich unmittelbar aus der Monotonie
und der Linearität des Erwartungswertes (vgl.
Theorem 4.4), denn es gilt
- Zu 4:
 Für
Für 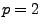 ergibt sich aus der
Minkowski-Ungleichung (4.68), dass
Hieraus folgt die vierte Teilaussage.
ergibt sich aus der
Minkowski-Ungleichung (4.68), dass
Hieraus folgt die vierte Teilaussage.

- Beachte
-
- Eine zu Theorem 5.8 analoge Aussage gilt im
allgemeinen nicht für die Konvergenz in Verteilung, d.h.,
aus
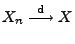 und
und
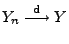 folgt im allgemeinen nicht, dass
folgt im allgemeinen nicht, dass
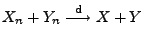 .
.
- Unter der zusätzlichen Annahme, dass
 oder
oder 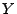 (mit
Wahrscheinlichkeit 1) konstante Größen sind, kann man jedoch
zeigen, dass auch die Konvergenz in Verteilung bei der Addition
von Zufallsvariablen erhalten bleibt. Gemeint ist die folgende
Aussage, die in der Literatur Satz von Slutsky genannt wird.
(mit
Wahrscheinlichkeit 1) konstante Größen sind, kann man jedoch
zeigen, dass auch die Konvergenz in Verteilung bei der Addition
von Zufallsvariablen erhalten bleibt. Gemeint ist die folgende
Aussage, die in der Literatur Satz von Slutsky genannt wird.
Theorem 5.9
Seien
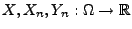
beliebige Zufallsvariablen über
einunddemselben Wahrscheinlichkeitsraum
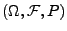
, und
sei
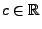
. Dann gilt

, falls
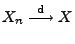
und
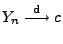
.
- Beweis
-
- Beachte
-
- Ähnlich wie bei der Addition von Zufallsvariablen (vgl.
Theorem 5.8) bleibt die fast sichere Konvergenz und
die Konvergenz in Wahrscheinlichkeit bei der Multiplikation von
Zufallsvariablen erhalten.
- Die Konvergenz im quadratischen Mittel geht jedoch im allgemeinen
bei der Produktbildung verloren; vgl. das folgende
Theorem 5.10.
- Beweis

- Zu 1:
 Falls
Falls
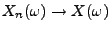 und
und
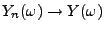 für ein
für ein
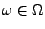 , dann gilt auch
, dann gilt auch
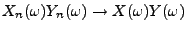 . Hieraus folgt die
erste Teilaussage.
. Hieraus folgt die
erste Teilaussage.
- Zu 2:
-
- Es gelte
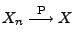 und
und
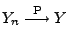 .
.
- Aus Theorem 5.2 folgt dann, dass es für jede
Teilfolge
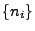 von
von
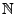 eine Teilfolge
eine Teilfolge
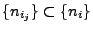 gibt, so dass
gibt, so dass
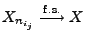 und
und
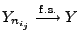 .
.
- Aus Teilaussage 1 ergibt sich somit, dass
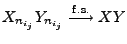 .
.
- Die erneute Anwendung von Theorem 5.2 zeigt nun,
dass
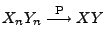 .
.
- Zu 3:
-
Die folgende Aussage wird Satz von Slutsky über die
Erhaltung der Verteilungskonvergenz bei der Multiplikation von
Zufallsvariablen genannt.
Theorem 5.11
Seien
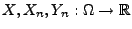
beliebige Zufallsvariablen über
einunddemselben Wahrscheinlichkeitsraum
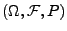
, und
sei
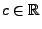
. Dann gilt
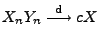
, falls
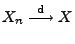
und
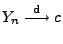
.
- Beweis
-
Wir zeigen nun noch, dass die fast sichere Konvergenz, die
Konvergenz in Wahrscheinlichkeit und die Konvergenz in Verteilung
bei der stetigen Abbildung von Zufallsvariablen erhalten bleiben.
Aussagen dieses Typs werden in der Literatur Continuous
Mapping Theorem genannt.
- Beweis

- Zu 1:
 Falls
Falls
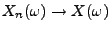 für ein
für ein
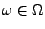 ,
dann gilt wegen der Stetigkeit von
,
dann gilt wegen der Stetigkeit von 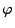 auch
auch
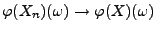 . Hieraus folgt die
erste Teilaussage.
. Hieraus folgt die
erste Teilaussage.
- Zu 2:
-
- Es gelte
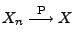 .
.
- Aus Theorem 5.2 folgt dann, dass es für jede
Teilfolge
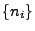 von
von
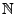 eine Teilfolge
eine Teilfolge
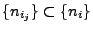 gibt, so dass
gibt, so dass
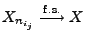 .
.
- Hieraus und aus Teilaussage 1 folgt, dass
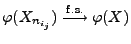 .
.
- Durch die erneute Anwendung von Theorem 5.2 ergibt
sich nun, dass
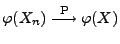 .
.
- Zu 3:





Next: Gesetz der großen Zahlen
Up: Konvergenzarten
Previous: Charakterisierung der Verteilungskonvergenz
Contents
Ursa Pantle
2004-05-10
![]() -Konvergenz und die
Konvergenz im quadratischen Mittel bei der Addition von
Zufallsvariablen erhalten bleiben.
-Konvergenz und die
Konvergenz im quadratischen Mittel bei der Addition von
Zufallsvariablen erhalten bleiben.
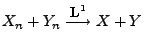 , falls
, falls
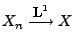 und
und
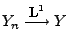 ,
,
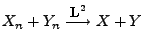 , falls
, falls
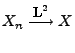 und
und
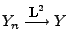 .
.
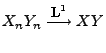 , falls
, falls
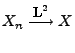 und
und
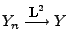
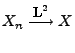 und
und
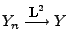 .
.
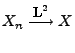 und
und 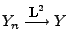 bzw. weil
bzw. weil
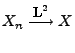 folgt und somit
folgt und somit