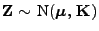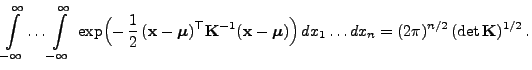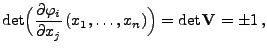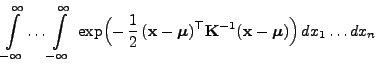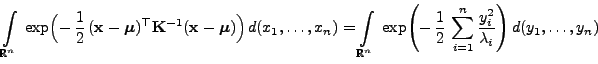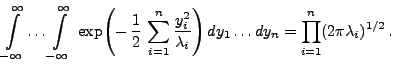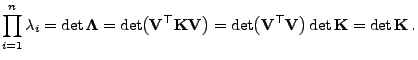wobei
wobei
- Sei
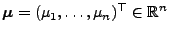 ein beliebiger
Vektor, und sei
ein beliebiger
Vektor, und sei
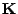 eine symmetrische und positiv definite
eine symmetrische und positiv definite
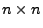 -Matrix.
-Matrix.
- Sei
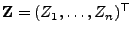 ein absolutstetiger
Zufallsvektor, wobei die gemeinsame Dichte von
ein absolutstetiger
Zufallsvektor, wobei die gemeinsame Dichte von
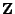 gegeben sei
durch
gegeben sei
durch
für jedes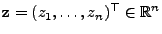 .
.
- Dann sagt man, dass der Zufallsvektor
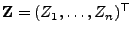 (regulär) normalverteilt ist.
(regulär) normalverteilt ist.
- Schreibweise: