



Nächste Seite: Schätzbare Funktionen
Aufwärts: Schätzung der Modellparameter
Vorherige Seite: KQ-Schätzer für
Inhalt
Erwartungswertvektor und
Kovarianzmatrix des KQ-Schätzers
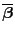
Aus den Modellannahmen (3) über die Störgrößen
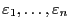 und aus den allgemeinen Rechenregeln für den
Erwartungswert bzw. die Kovarianz von reellwertigen
Zufallsvariablen ergibt sich, dass Erwartungswertvektor und
Kovarianzmatrix des KQ-Schätzers
und aus den allgemeinen Rechenregeln für den
Erwartungswert bzw. die Kovarianz von reellwertigen
Zufallsvariablen ergibt sich, dass Erwartungswertvektor und
Kovarianzmatrix des KQ-Schätzers
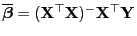 die
folgende Form haben.
die
folgende Form haben.
- Beweis
-
- Aus
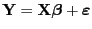 und
und
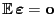 ergibt
sich, dass
ergibt
sich, dass
- Außerdem gilt für beliebige
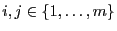

Aus den Theoremen 3.5 und 3.7 ergibt
sich mit Hilfe von Lemma 3.2, dass es keinen
KQ-Schätzer für
 gibt, der gleichzeitig erwartungstreu
ist. Insbesondere ist der in (38) gegebene
KQ-Schätzer
gibt, der gleichzeitig erwartungstreu
ist. Insbesondere ist der in (38) gegebene
KQ-Schätzer
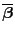 für
für
 nicht
erwartungstreu.
nicht
erwartungstreu.
Theorem 3.8

Wenn
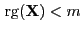
, dann gibt
es keinen erwartungstreuen KQ-Schätzer für

.
- Beweis
-
- Wegen
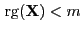 ergibt sich aus Lemma 3.2, dass
auch
ergibt sich aus Lemma 3.2, dass
auch
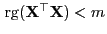 bzw.
bzw.
- Weil (41) nicht für jedes
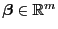 gilt,
ergibt sich darüber hinaus, dass auch für jedes beliebige, jedoch
fest vorgegebene
gilt,
ergibt sich darüber hinaus, dass auch für jedes beliebige, jedoch
fest vorgegebene
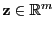 die Gleichung
bzw.
nicht für jedes
die Gleichung
bzw.
nicht für jedes
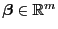 gilt.
gilt.
- Wegen Theorem 3.5 bedeutet dies, dass es keinen
KQ-Schätzer für
 gibt, der gleichzeitig erwartungstreu
ist.
gibt, der gleichzeitig erwartungstreu
ist.





Nächste Seite: Schätzbare Funktionen
Aufwärts: Schätzung der Modellparameter
Vorherige Seite: KQ-Schätzer für
Inhalt
Hendrik Schmidt
2006-02-27
![]() und aus den allgemeinen Rechenregeln für den
Erwartungswert bzw. die Kovarianz von reellwertigen
Zufallsvariablen ergibt sich, dass Erwartungswertvektor und
Kovarianzmatrix des KQ-Schätzers
und aus den allgemeinen Rechenregeln für den
Erwartungswert bzw. die Kovarianz von reellwertigen
Zufallsvariablen ergibt sich, dass Erwartungswertvektor und
Kovarianzmatrix des KQ-Schätzers
![]() die
folgende Form haben.
die
folgende Form haben.
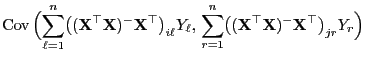
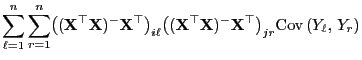
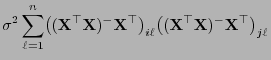
![]() gibt, der gleichzeitig erwartungstreu
ist. Insbesondere ist der in (38) gegebene
KQ-Schätzer
gibt, der gleichzeitig erwartungstreu
ist. Insbesondere ist der in (38) gegebene
KQ-Schätzer
![]() für
für
![]() nicht
erwartungstreu.
nicht
erwartungstreu.