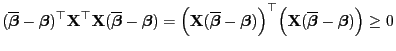Nächste Seite: Erwartungswertvektor und Kovarianzmatrix des
Aufwärts: Schätzung der Modellparameter
Vorherige Seite: Schätzung der Modellparameter
Inhalt
KQ-Schätzer für

Die folgende Eigenschaft des Ranges von Matrixprodukten ist
nützlich, die sich unmittelbar aus der in Lemma 2.3
betrachteten Rangformel ergibt.
Lemma 3.2
Seien
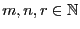
beliebige natürliche Zahlen, und seien
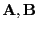
beliebige
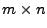
bzw.
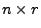
Matrizen.
Dann gilt
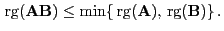 |
(23) |
- Beachte
-
- Weil wir jetzt annehmen, dass die Designmatrix
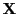 keinen
vollen Rang besitzt, ist die
keinen
vollen Rang besitzt, ist die 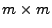 Matrix
Matrix
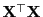 nicht invertierbar, denn gemäß Lemma 3.2
gilt
nicht invertierbar, denn gemäß Lemma 3.2
gilt
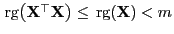 .
.
- Die Normalengleichung (2.9), d.h.,
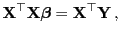 |
(24) |
besitzt
deshalb keine eindeutig bestimmte Lösung.
- Um die Lösungsmenge der Gleichung (24) zu
beschreiben, benötigen wir den Begriff der verallgemeinerten
inversen Matrix, vgl. auch Abschnitt 3.4 der Vorlesung
,,Numerik 1a'' von K. Urban (Universität Ulm, Sommersemester
2005).
- Definition
 Eine
Eine 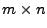 Matrix
Matrix
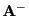 heißt
verallgemeinerte Inverse der
heißt
verallgemeinerte Inverse der 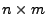 Matrix
Matrix
 ,
wenn
,
wenn
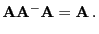 |
(25) |
Um zu zeigen, dass es immer eine Lösung
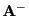 der
Definitionsgleichung (25) gibt, benutzen wir die
folgende allgemeine Matrix-Darstellungsformel, die wir hier ohne
Beweis angeben.
der
Definitionsgleichung (25) gibt, benutzen wir die
folgende allgemeine Matrix-Darstellungsformel, die wir hier ohne
Beweis angeben.
Lemma 3.3

Sei

eine
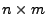
Matrix mit
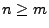
und
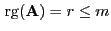
. Dann gibt es invertierbare
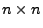
bzw.
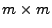
Matrizen
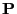
bzw.
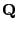
, so dass
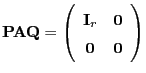 bzw. bzw.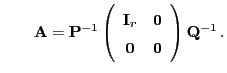 |
(26) |
Mit Hilfe von Lemma 3.3 kann man zeigen, wie man zu
Lösungen
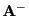 von (25) gelangen kann.
von (25) gelangen kann.
Insgesamt erhalten wir somit das folgende Ergebnis.
Lemma 3.4
Sei

eine
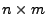
Matrix mit
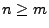
und
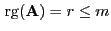
. Außerdem sei
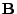
für jedes
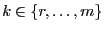
die in
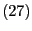
-
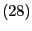
gegebene
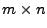
Matrix. Dann gilt
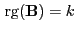
und
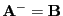
ist eine Lösung der Gleichung
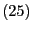
.
Außerdem sind die folgenden Eigenschaften der verallgemeinerten
Inversen nützlich.
- Beweis
-
- Definitionsgemäß gilt für die verallgemeinerte Inverse, dass
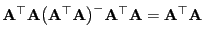 .
.
- Hieraus und aus der Symmetrie der Matrix
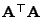 ergibt
sich, dass
d.h. die transponierte Matrix
ergibt
sich, dass
d.h. die transponierte Matrix
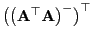 ist ebenfalls
eine verallgemeinerte Inverse von
ist ebenfalls
eine verallgemeinerte Inverse von
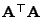 .
.
- Um die zweite Teilaussage (29) zu beweisen,
betrachten wir die Matrix
- Dann gilt
- Hieraus folgt, dass
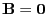 .
.

Mit Hilfe der verallgemeinerten Inversen
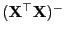 von
von
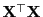 und ihrer (in Lemma 3.5
betrachteten) Eigenschaften lässt sich die Lösungsmenge der
Normalengleichung (24) beschreiben.
und ihrer (in Lemma 3.5
betrachteten) Eigenschaften lässt sich die Lösungsmenge der
Normalengleichung (24) beschreiben.
Theorem 3.5
Die allgemeine Lösung

der Normalengleichung
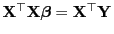
hat die Form
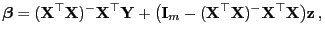 |
(30) |
wobei
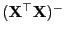
eine beliebige Lösung der Gleichung
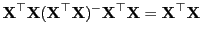 |
(31) |
und
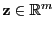
ein beliebiger
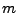
-dimensionaler Vektor ist.
- Beweis
-
- Beispiel
 (einfaktorielle Varianzanalyse)
(einfaktorielle Varianzanalyse)
- Zur Erinnerung: Im reparametrisierten Modell der
einfaktoriellen Varianzanalyse (vgl. Fall
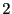 des in
Abschnitt 3.1.2 betrachteten Beispiels) ist die
Designmatrix gegeben durch die
des in
Abschnitt 3.1.2 betrachteten Beispiels) ist die
Designmatrix gegeben durch die
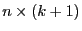 Matrix
Matrix
 |
(33) |
und der Parametervektor
 ist gegeben durch
ist gegeben durch
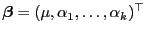 .
.
- Man kann sich leicht überlegen, dass dann
 |
(34) |
und dass eine verallgemeinerte Inverse von
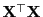 gegeben ist durch
gegeben ist durch
 |
(35) |
- Die Normalengleichung (24), d.h.
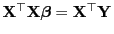 , besitzt somit die
folgende Gestalt:
, besitzt somit die
folgende Gestalt:
- Wenn wir die Lösungen dieses Gleichungssystems lediglich in dem
eingeschränkten Parameterraum
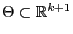 suchen, wobei
suchen, wobei
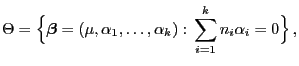 |
(36) |
dann ergibt sich die (eindeutig bestimmte) Lösung
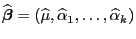 mit
mit
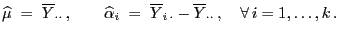 |
(37) |
- Man kann sich leicht überlegen, dass die in (37)
gegebene Lösung
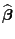 der Normalengleichung
(24)
der Normalengleichung
(24)
- die Gestalt
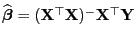 hat, wobei die verallgemeinerte Inverse
hat, wobei die verallgemeinerte Inverse
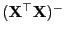 durch (35) gegeben ist, und
durch (35) gegeben ist, und
- ein erwartungstreuer Schätzer für
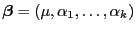 bezüglich des
eingeschränkten Parameterraumes
bezüglich des
eingeschränkten Parameterraumes 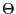 ist, der die in
(36) gegebene Form hat.
ist, der die in
(36) gegebene Form hat.
- Ohne die in (36) betrachtete Nebenbedingung gibt es
jedoch keinen KQ-Schätzer für
 , der gleichzeitig
erwartungstreu ist, vgl. Theorem 3.8.
, der gleichzeitig
erwartungstreu ist, vgl. Theorem 3.8.
Wir betrachten jetzt erneut das in (1) -
(3) gegebene lineare Modell mit allgemeiner
Designmatrix
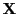 . Insbesondere betrachten wir die in
Theorem 3.5 diskutierten Lösungen der
Normalengleichung (24) und zeigen, dass für
. Insbesondere betrachten wir die in
Theorem 3.5 diskutierten Lösungen der
Normalengleichung (24) und zeigen, dass für
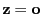 der in
der in
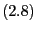 gegebene mittlere
quadratische Fehler
gegebene mittlere
quadratische Fehler
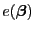 minimiert wird.
minimiert wird.
Theorem 3.6

Sei
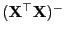
eine beliebige verallgemeinerte
Inverse von
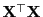
. Dann minimiert die
Stichprobenfunktion
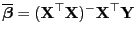 |
(38) |
den mittleren quadratischen Fehler
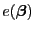
, d.h.,
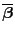
ist ein KQ-Schätzer für

.
- Beweis
-
- Für jeden
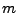 -dimensionalen Vektor
-dimensionalen Vektor
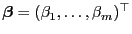 gilt
gilt
weil
und
wobei sich die letzte Gleichheit aus Lemma 3.5
ergibt.





Nächste Seite: Erwartungswertvektor und Kovarianzmatrix des
Aufwärts: Schätzung der Modellparameter
Vorherige Seite: Schätzung der Modellparameter
Inhalt
Hendrik Schmidt
2006-02-27
![]() der
Definitionsgleichung (25) gibt, benutzen wir die
folgende allgemeine Matrix-Darstellungsformel, die wir hier ohne
Beweis angeben.
der
Definitionsgleichung (25) gibt, benutzen wir die
folgende allgemeine Matrix-Darstellungsformel, die wir hier ohne
Beweis angeben.
![]() von (25) gelangen kann.
von (25) gelangen kann.
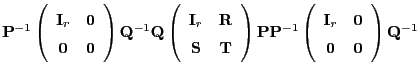
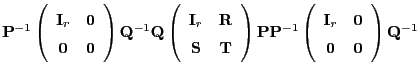
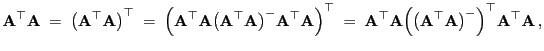
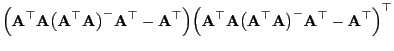
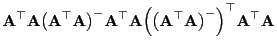
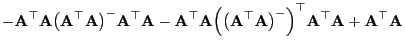
![]() von
von
![]() und ihrer (in Lemma 3.5
betrachteten) Eigenschaften lässt sich die Lösungsmenge der
Normalengleichung (24) beschreiben.
und ihrer (in Lemma 3.5
betrachteten) Eigenschaften lässt sich die Lösungsmenge der
Normalengleichung (24) beschreiben.
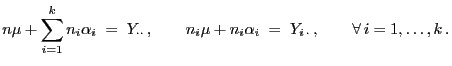
![]() . Insbesondere betrachten wir die in
Theorem 3.5 diskutierten Lösungen der
Normalengleichung (24) und zeigen, dass für
. Insbesondere betrachten wir die in
Theorem 3.5 diskutierten Lösungen der
Normalengleichung (24) und zeigen, dass für
![]() der in
der in
![]() gegebene mittlere
quadratische Fehler
gegebene mittlere
quadratische Fehler
![]() minimiert wird.
minimiert wird.