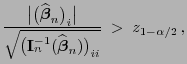- Sei
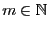 eine beliebige natürliche Zahl, und
seien
eine beliebige natürliche Zahl, und
seien
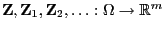 beliebige
Zufallsvektoren. Man sagt, dass
beliebige
Zufallsvektoren. Man sagt, dass
 in Verteilung
gegen
in Verteilung
gegen
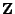 konvergiert, wenn
konvergiert, wenn
für jedes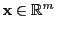 mit
mit
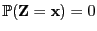 . Schreibweise:
. Schreibweise:
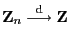 .
.
- Dabei betrachten wir lediglich den Fall der natürlichen
Linkfunktion

- und indizieren die Zufallsstichprobe
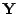 , die
Loglikelihood-Funktion
, die
Loglikelihood-Funktion
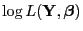 , den Scorevektor
, den Scorevektor
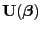 , die Fisher-Informationsmatrix
, die Fisher-Informationsmatrix
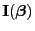 bzw. den ML-Schätzer
bzw. den ML-Schätzer
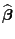 jeweils
mit
jeweils
mit  .
.