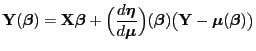Nächste Seite: Asymptotische Normalverteiltheit von ML-Schätzern;
Aufwärts: Maximum-Likelihood-Schätzer für
Vorherige Seite: Hesse-Matrix
Inhalt
Maximum-Likelihood-Gleichung und numerische Lösungsansätze
- Zur Bestimmung eines Maximum-Likelihood-Schätzers für
 wird die Maximum-Likelihood-Gleichung
wird die Maximum-Likelihood-Gleichung
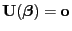 |
(39) |
betrachtet, die im allgemeinen nichtlinear
ist und deshalb oft nur mit iterativen Methoden gelöst werden
kann.
- Wegen Theorem 4.1 ist die Gleichung
(39) äquivalent mit
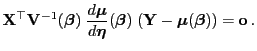 |
(40) |
- Beachte
-
Wir diskutieren nun die Grundideen von zwei numerischen
Iterationsmethoden zur
Lösung der Maximum-Likelihood-Gleichung
(39). Dabei betrachten wir eine Folge von
Zufallsvektoren
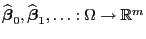 , die
unter gewissen Bedingungen gegen einen Zufallsvektor
, die
unter gewissen Bedingungen gegen einen Zufallsvektor
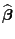 konvergieren, so dass
konvergieren, so dass
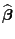 Lösung
von (39) ist.
Lösung
von (39) ist.
- 1.
- Newton-Verfahren
- 2.
- Fisher-Scoring
- Wir betrachten nun eine Variante des Newton-Verfahrens, die so
genannte Scoring-Methode von Fisher, bei der die
Hesse-Matrix
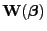 in (42) durch die
Erwartungswertmatrix
in (42) durch die
Erwartungswertmatrix
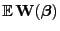 ersetzt wird.
ersetzt wird.
- Anstelle von (43) wird somit die folgende
Iterationsgleichung betrachtet:
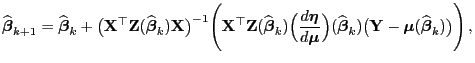 |
(44) |
wobei
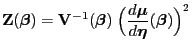
und
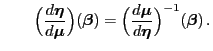
- Bei natürlicher Linkfunktion ergibt sich aus
Lemma 4.2, dass
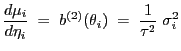
bzw.
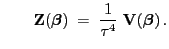
- In diesem Fall hat dann die Iterationsgleichung
(44) die Form:
- Beachte
-
- Wenn in (44) die Zufallsstichprobe
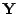 durch
die so genannte Pseudo-Zufallsstichprobe
ersetzt wird, dann lässt sich die Iterationsgleichung
(44) in der folgenden Form schreiben:
durch
die so genannte Pseudo-Zufallsstichprobe
ersetzt wird, dann lässt sich die Iterationsgleichung
(44) in der folgenden Form schreiben:
- Diese Gleichung kann als gewichtete Normalengleichung für
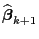 bezüglich der Pseudo-Zufallsstichprobe
bezüglich der Pseudo-Zufallsstichprobe
 aufgefasst werden, wobei die Gewichte,
d.h., die Eintragungen der Diagonalmatrix
aufgefasst werden, wobei die Gewichte,
d.h., die Eintragungen der Diagonalmatrix
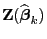 ebenfalls von der
ebenfalls von der 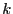 -ten Iteration
-ten Iteration
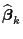 abhängen.
abhängen.




Nächste Seite: Asymptotische Normalverteiltheit von ML-Schätzern;
Aufwärts: Maximum-Likelihood-Schätzer für
Vorherige Seite: Hesse-Matrix
Inhalt
Hendrik Schmidt
2006-02-27
![]() , die
unter gewissen Bedingungen gegen einen Zufallsvektor
, die
unter gewissen Bedingungen gegen einen Zufallsvektor
![]() konvergieren, so dass
konvergieren, so dass
![]() Lösung
von (39) ist.
Lösung
von (39) ist.
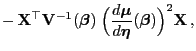
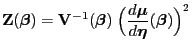 und
und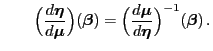
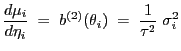 bzw.
bzw.