



Nächste Seite: -Anpassungstest
Aufwärts: Kolmogorow-Smirnow-Test
Vorherige Seite: Asymptotische Verteilung
Inhalt
Güteeigenschaften; punktweise und gleichmäßige Konsistenz
In diesem Abschnitt betrachten wir einige Güteeigenschaften des
Kolmogorow-Smirnow-Tests.
Um die (punktweise) Konsistenz des KS-Tests zu zeigen, benötigen
wir den Satz von Gliwenko-Cantelli (vgl. Theorem I-1.18),
d.h., dass
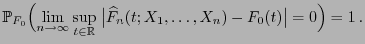 |
(17) |
Theorem 5.2

Die Verteilungsfunktion
![$ F_0:\mathbb{R}\to[0,1]$](img1875.png)
sei stetig. Dann ist der
Kolmogorow-Smirnow-Test punktweise konsistent für jede
Verteilungsfunktion
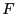
der Stichprobenvariablen mit
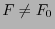
,
d.h., es gilt
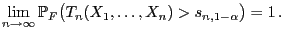 |
(18) |
- Beweis
-
- Beachte
-
Lemma 5.3

Für beliebige
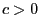
und
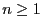
gilt
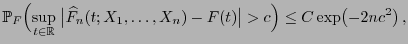 |
(20) |
wobei
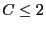
eine universelle Konstante ist, die nicht von
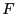
abhängt.
- Beachte
-
Mit diesen Hilfsmitteln können wir die bereits oben erwähnte
gleichmäßige Konsistenz-Eigenschaft des KS-Tests für den Fall
zeigen, dass der Kolmogorow-Abstand
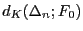 zwischen
der Familie
zwischen
der Familie 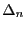 der alternativen Verteilungsfunktionen und
der (hypothetischen) Verteilungsfunktion
der alternativen Verteilungsfunktionen und
der (hypothetischen) Verteilungsfunktion 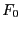 mit wachsendem
Stichprobenumfang
mit wachsendem
Stichprobenumfang  nicht zu schnell gegen 0 konvergiert.
nicht zu schnell gegen 0 konvergiert.
Theorem 5.3

Wenn es eine Folge
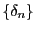
positiver Zahlen mit
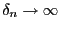
gibt, so dass
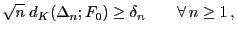 |
(23) |
dann gilt
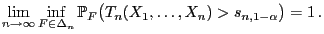 |
(24) |
- Beweis
-
- Sei
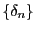 eine Folge positiver Zahlen mit
eine Folge positiver Zahlen mit
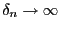 , für die (23) gilt, und sei
, für die (23) gilt, und sei
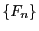 eine beliebige Folge von Verteilungsfunktionen, so dass
für jedes
eine beliebige Folge von Verteilungsfunktionen, so dass
für jedes 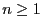
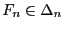 und somit und somit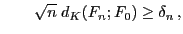 |
(25) |
wobei
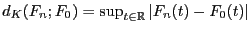 .
.
- Es genügt zu zeigen, dass
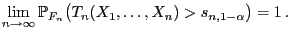 |
(26) |
- Aus der Dreiecksungleichung ergibt sich, dass
- Hieraus und aus (25) folgt, dass
- Folglich gilt
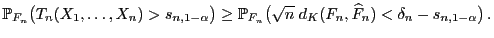 |
(27) |
- Weil
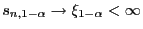 und somit
und somit
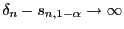 für
für
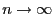 , ergibt sich
die Gültigkeit von (26) aus (22) und
(27).
, ergibt sich
die Gültigkeit von (26) aus (22) und
(27).

- Beachte
-
Andererseits kann die (asymptotische) Macht des KS-Tests beliebig
klein werden, d.h., beliebig nahe bei 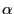 sein, wenn der
Kolmogorow-Abstand
sein, wenn der
Kolmogorow-Abstand
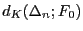 zwischen der Familie
zwischen der Familie
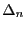 der alternativen Verteilungsfunktionen und der
(hypothetischen) Verteilungsfunktion
der alternativen Verteilungsfunktionen und der
(hypothetischen) Verteilungsfunktion 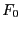 mit wachsendem
Stichprobenumfang
mit wachsendem
Stichprobenumfang  hinreichend schnell gegen 0 konvergiert.
hinreichend schnell gegen 0 konvergiert.
Theorem 5.4
- Sei
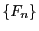 eine beliebige Folge
von stetigen Verteilungsfunktionen, so dass
eine beliebige Folge
von stetigen Verteilungsfunktionen, so dass
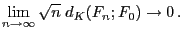 |
(29) |
- Dann gilt
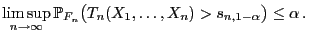 |
(30) |
- Beweis
-




Nächste Seite: -Anpassungstest
Aufwärts: Kolmogorow-Smirnow-Test
Vorherige Seite: Asymptotische Verteilung
Inhalt
Hendrik Schmidt
2006-02-27
![]() zwischen
der Familie
zwischen
der Familie ![]() der alternativen Verteilungsfunktionen und
der (hypothetischen) Verteilungsfunktion
der alternativen Verteilungsfunktionen und
der (hypothetischen) Verteilungsfunktion ![]() mit wachsendem
Stichprobenumfang
mit wachsendem
Stichprobenumfang ![]() nicht zu schnell gegen 0 konvergiert.
nicht zu schnell gegen 0 konvergiert.
![]() sein, wenn der
Kolmogorow-Abstand
sein, wenn der
Kolmogorow-Abstand
![]() zwischen der Familie
zwischen der Familie
![]() der alternativen Verteilungsfunktionen und der
(hypothetischen) Verteilungsfunktion
der alternativen Verteilungsfunktionen und der
(hypothetischen) Verteilungsfunktion ![]() mit wachsendem
Stichprobenumfang
mit wachsendem
Stichprobenumfang ![]() hinreichend schnell gegen 0 konvergiert.
hinreichend schnell gegen 0 konvergiert.