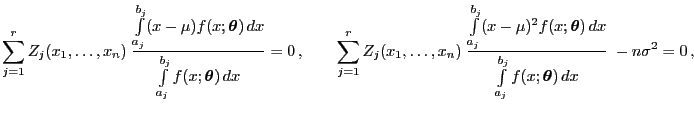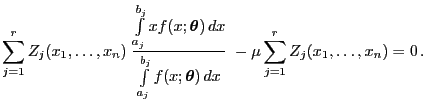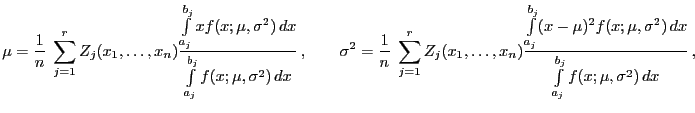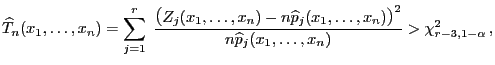Nächste Seite: Anpassungstests vom Shapiro-Wilk-Typ
Aufwärts: Beispiele
Vorherige Seite: -Anpassungstest auf Poisson-Verteilung
Inhalt
- Sei nun
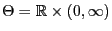 mit
mit
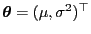 , und sei
, und sei
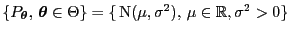 die Familie der
(eindimensionalen) Normalverteilungen.
die Familie der
(eindimensionalen) Normalverteilungen.
- Die Wahrscheinlichkeiten
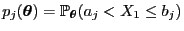 sind dann gegeben durch
sind dann gegeben durch
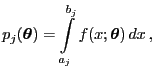 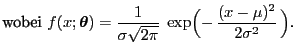 |
(83) |
- Gemäß (66) genügt jede
Maximum-Likelihood-Schätzung
für
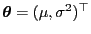 , die aus den gruppierten Daten
gewonnen wird, dem Gleichungssystem
, die aus den gruppierten Daten
gewonnen wird, dem Gleichungssystem
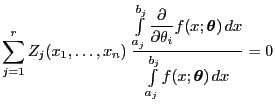 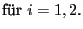 |
(84) |
- Dabei ergibt sich aus (83), dass
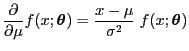
bzw.
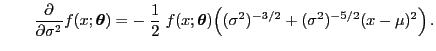
- Hieraus und aus (84) folgt, dass die ML-Schätzung
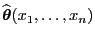 dem folgenden Gleichungssystem
genügt:
wobei die erste Gleichung dieses Gleichungssystems äquivalent ist
mit
dem folgenden Gleichungssystem
genügt:
wobei die erste Gleichung dieses Gleichungssystems äquivalent ist
mit
- Die ML-Schätzung
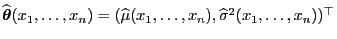 genügt deshalb dem
Gleichungssystem
genügt deshalb dem
Gleichungssystem
- Die Nullhypothese
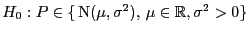 wird abgelehnt, wenn
wobei
wird abgelehnt, wenn
wobei
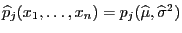 mit der in
(83)) gegebenen Funktion
mit der in
(83)) gegebenen Funktion
![$ p_j:\mathbb{R}\times(0,\infty)\to[0,1]$](img2306.png) und der in (85)
gegebenen Schätzung
und der in (85)
gegebenen Schätzung
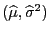 für
für
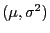 .
.
- Beachte
-
- Die Näherungslösung (85) des Gleichungssystems
(84) sollte nur dann verwendet werden, wenn die
Anzahl
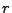 der Klassen hinreichend groß ist.
der Klassen hinreichend groß ist.
- Dies setzt einen hinreichend großen Stichprobenumfang
 voraus.
voraus.
- Mit anderen Worten: Wenn der Stichprobenumfang
 klein ist, dann
ist der
klein ist, dann
ist der  -Anpassungstest auch aus diesem Grund nicht
geeignet, um die Hypothese der Normalverteiltheit zu verifizieren.
-Anpassungstest auch aus diesem Grund nicht
geeignet, um die Hypothese der Normalverteiltheit zu verifizieren.
- Alternative Tests auf Normalverteilung sind die folgenden Anpassungstests vom Shapiro-Wilk-Typ, die auch bei kleinem
Stichprobenumfang
 zu akzeptablen Ergebnissen führen.
zu akzeptablen Ergebnissen führen.




Nächste Seite: Anpassungstests vom Shapiro-Wilk-Typ
Aufwärts: Beispiele
Vorherige Seite: -Anpassungstest auf Poisson-Verteilung
Inhalt
Hendrik Schmidt
2006-02-27