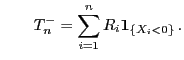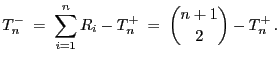- Am Ende von Abschnitt 6.1.1 hatten wir im Zusammenhang
mit dem Binomial- bzw. Vorzeichentest einen Mediantest
diskutiert, um die Hypothese
zu verifizieren, wobei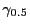 ein Median von
ein Median von 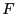 ist, d.h.,
ist, d.h.,
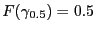 .
.
- In diesem Abschnitt betrachten wir einen weiteren (effizienteren) Ansatz, um die in (9) gegebene Hypothese zu testen.
- Sei
![$ G:\mathbb{R}\to[0,1]$](img2461.png) eine beliebige stetige Verteilungsfunktion,
die die folgende Symmetrieeigenschaft bezüglich des Nullpunktes
besitzt: Für jedes
eine beliebige stetige Verteilungsfunktion,
die die folgende Symmetrieeigenschaft bezüglich des Nullpunktes
besitzt: Für jedes
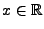 gelte
gelte
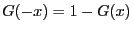 .
.
- Hieraus folgt insbesondere, dass
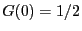 , d.h., der Nullpunkt
ist ein Median von
, d.h., der Nullpunkt
ist ein Median von 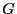 .
.
- Die Familie
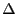 von Verteilungsfunktionen der
Stichprobenvariablen
von Verteilungsfunktionen der
Stichprobenvariablen
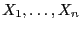 , die beim (zweiseitigen)
Wilcoxon-Test in Betracht gezogenen wird, sei gegeben durch
, die beim (zweiseitigen)
Wilcoxon-Test in Betracht gezogenen wird, sei gegeben durch
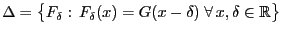 .
.
- Weil
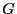 stetig ist, gilt dann für jedes
stetig ist, gilt dann für jedes
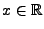 und für
beliebige
und für
beliebige
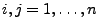 mit
mit 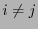
- Dabei können wir (o.B.d.A.)
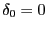 setzen; ansonsten können
die transformierten Stichprobenvariablen
setzen; ansonsten können
die transformierten Stichprobenvariablen
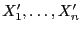 mit
mit
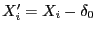 betrachtet werden.
betrachtet werden.
- Auf ähnliche Weise kann auch das (einseitige) Testproblem
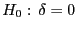 vs.
vs.
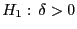 behandelt werden.
behandelt werden.
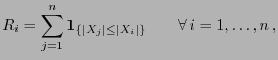
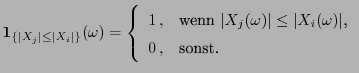
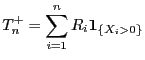 bzw.
bzw.