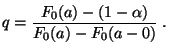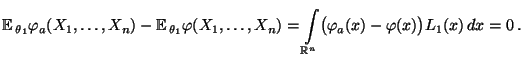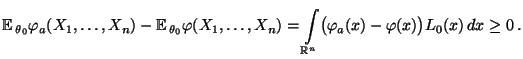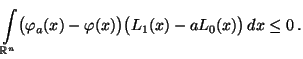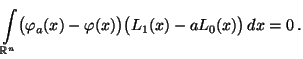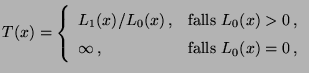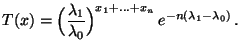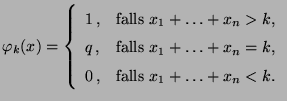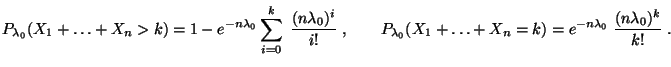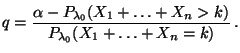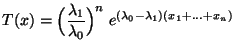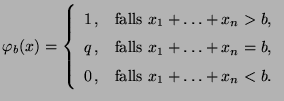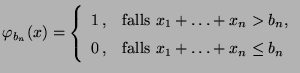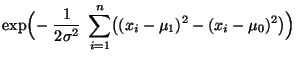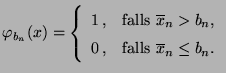Next: Konsistenz und relative Entropie
Up: Gleichmäßig beste Tests
Previous: Neyman-Pearson-Tests
Contents
Lemma von Neyman-Pearson
Außerdem kann man zeigen, daß es für jedes
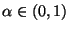 einen
NP-Test zum Niveau
einen
NP-Test zum Niveau 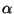 gibt, der dann gemäß
Theorem 4.1 bester Test in der Familie aller
(randomisierten) Tests zum Niveau
gibt, der dann gemäß
Theorem 4.1 bester Test in der Familie aller
(randomisierten) Tests zum Niveau 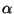 ist. Außerdem ist der
NP-Test zum Niveau
ist. Außerdem ist der
NP-Test zum Niveau 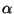 in einem gewissen Sinne eindeutig
bestimmt.
Dieser Existenz- und Eindeutigkeitssatz wird in der Literatur das
Fundamentallemma von Neyman-Pearson genannt; zu Ehren von
Jerzy Neyman (1894-1981) und Egon Pearson (1895-1980), der Sohn
des Statistikers Karl Pearson.
in einem gewissen Sinne eindeutig
bestimmt.
Dieser Existenz- und Eindeutigkeitssatz wird in der Literatur das
Fundamentallemma von Neyman-Pearson genannt; zu Ehren von
Jerzy Neyman (1894-1981) und Egon Pearson (1895-1980), der Sohn
des Statistikers Karl Pearson.
- Beweis
-
- Um die Gültigkeit von Teilaussage 1 zu beweisen, genügt es wegen
(29) zu zeigen, daß es reelle Zahlen
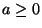 und
und
![$ q\in[0,1]$](img2217.png) gibt, so daß
gibt, so daß
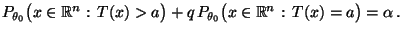 |
(33) |
- Sei
![$ F_0:\mathbb{R}\to[0,1]$](img2250.png) die Verteilungsfunktion von
die Verteilungsfunktion von 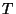 unter
unter 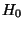 .
Dann ist (33) äquivalent mit
.
Dann ist (33) äquivalent mit
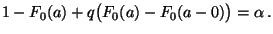 |
(34) |
- Sei
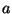 das
das
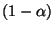 -Quantil von
-Quantil von 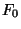 , d.h.,
, d.h.,
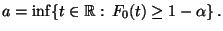 |
(35) |
- Dann gilt
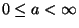 , denn wegen
, denn wegen
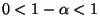 und
und
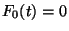 für
für  gilt
gilt 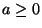 , und wegen
gilt auch
, und wegen
gilt auch 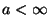 .
.
- Außerdem ergibt sich aus der Definitionsgleichung
(35) des
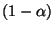 -Quantils
-Quantils 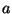 , daß
, daß
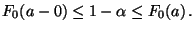 |
(36) |
- Falls
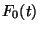 stetig im Punkt
stetig im Punkt 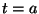 ist, d.h.
ist, d.h.
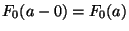 ,
dann ergibt sich aus (36), daß
,
dann ergibt sich aus (36), daß
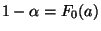 und daß somit (34) für jedes
und daß somit (34) für jedes ![$ q\in[0,1]$](img2217.png) gilt.
gilt.
- Falls
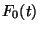 unstetig im Punkt
unstetig im Punkt 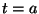 ist, d.h.
ist, d.h.
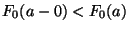 , dann gilt (34) für
, dann gilt (34) für
- Um die Gültigkeit von Teilaussage 2 zu beweisen, setzen wir
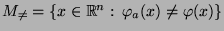 und
zeigen, daß
und
zeigen, daß
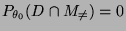 bzw. bzw.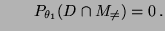 |
(37) |
- Wir betrachten nur den absolutstetigen Fall. Im diskreten Fall
ergibt sich die Behauptung auf analoge Weise, wobei lediglich die
Integrale in den folgenden Formeln durch entsprechende Summen zu
ersetzen sind.
- Weil
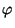 und
und 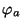 beste Tests sind, gilt
beste Tests sind, gilt
- Andererseits ergibt sich aus
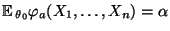 und
und
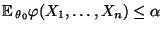 , daß
, daß
- Insgesamt ergibt sich somit, daß
- Zusammen mit (31) folgt hieraus,daß
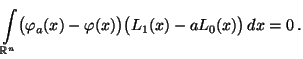 |
(38) |
- Andererseits gelten für jedes
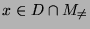 die folgenden
Implikationen:
die folgenden
Implikationen:

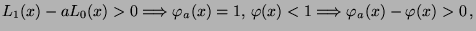

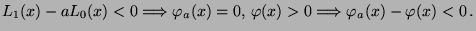
- Für jedes
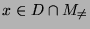 ist somit der Integrand in
(38) strikt positiv, während er für
ist somit der Integrand in
(38) strikt positiv, während er für
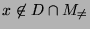 gleich 0 ist.
gleich 0 ist.
- Hieraus folgt, daß das Lebesque-Maß der Menge
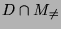 gleich 0 sein muß.
gleich 0 sein muß.

- Beispiele
-
 Poisson-verteilte Stichprobenvariablen
Poisson-verteilte Stichprobenvariablen
 Exponentialverteilte Stichprobenvariablen
Exponentialverteilte Stichprobenvariablen
- Sei
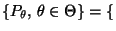 Exp
Exp
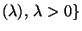 die Familie der Exponentialverteilungen.
die Familie der Exponentialverteilungen.
- Für zwei beliebige, jedoch vorgegebene Parameterwerte
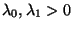 mit
mit
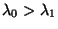 konstruieren wir
einen NP-Test zur Verifizierung der (einfachen) Hypothesen
konstruieren wir
einen NP-Test zur Verifizierung der (einfachen) Hypothesen
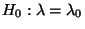
versus
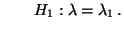
- Für den in (28) eingeführten Likelihood-Quotienten
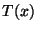 gilt dann
für beliebige
gilt dann
für beliebige
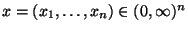 .
.
- Weil die rechte Seite dieses Ausdruckes erneut eine streng monoton
wachsende Funktion der Summe
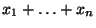 der Stichprobenwerte
der Stichprobenwerte
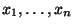 ist, läßt sich der Ablehnungsbereich
ist, läßt sich der Ablehnungsbereich 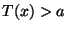 bzw. der Randomisierungsbereich
bzw. der Randomisierungsbereich 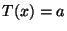 durch einen Schwellenwert
durch einen Schwellenwert
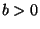 der Summe
der Summe
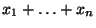 ausdrücken.
ausdrücken.
- Der NP-Test
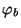 zum Niveau
zum Niveau 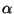 hat dann die Form
hat dann die Form
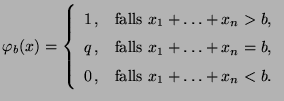 |
(40) |
- Weil die Zufallsvariable
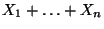 unter
unter 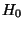 gammaverteilt ist mit
gammaverteilt ist mit
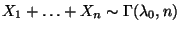 ,
gilt
Die Zahl
,
gilt
Die Zahl ![$ q\in[0,1]$](img2217.png) kann deshalb beliebig (zum Beispiel
kann deshalb beliebig (zum Beispiel 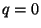 )
gewählt werden.
)
gewählt werden.
- Für
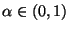 wird
wird 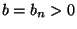 dann aus der Gleichung
dann aus der Gleichung
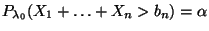 |
(41) |
bestimmt, d.h., 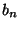 ist das
ist das
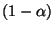 -Quantil der
-Quantil der
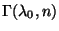 -Verteilung.
-Verteilung.
- Beachte: Die Lösung
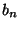 der Gleichung (41)
hängt nicht von
der Gleichung (41)
hängt nicht von 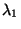 ab. Außerdem gilt
und
ab. Außerdem gilt
und
- Man kann zeigen, daß dann auch für die Prüfung der
(zusammengesetzten) Hypothesen
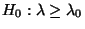
versus
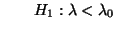
ein gleichmäßig bester (unverfälschter)
Test zum Niveau 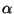 durch die Stichprobenfunktion
durch die Stichprobenfunktion
![$ \varphi_{b_n}:(0,\infty)^n\to[0,1]$](img2317.png) mit
mit
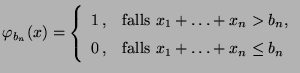 |
(42) |
gegeben ist, wobei 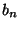 das
das
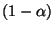 -Quantil der
-Quantil der
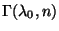 -Verteilung ist; vgl.
Abschnitt 4.5.6.
-Verteilung ist; vgl.
Abschnitt 4.5.6.
- Aus dem starken Gesetz der großen Zahlen (vgl. Theorem WR-5.15)
ergibt sich die Gültigkeit von
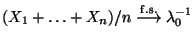 unter
unter
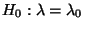 .
.
- Hieraus und aus (41) folgt somit, daß
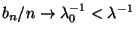 für
für
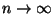 .
.
- Die erneute Anwendung des starken Gesetzes der großen Zahlen
ergibt nun, daß für jedes
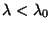
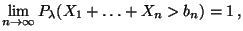 |
(43) |
d.h., der in (42) gegebene Test ist konsistent.
 Normalverteilte Stichprobenvariablen
Normalverteilte Stichprobenvariablen
- Beachte
 Die Frage, wie schnell die Konvergenz in (43) bzw.
(46) erfolgt, d.h., wie schnell die
Wahrscheinlichkeit des Fehlers zweiter Art bei wachsendem
Stichprobenumfang
Die Frage, wie schnell die Konvergenz in (43) bzw.
(46) erfolgt, d.h., wie schnell die
Wahrscheinlichkeit des Fehlers zweiter Art bei wachsendem
Stichprobenumfang 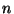 gegen 0 konvergiert, werden wir in
Abschnitt 4.5.4 näher untersuchen.
gegen 0 konvergiert, werden wir in
Abschnitt 4.5.4 näher untersuchen.




Next: Konsistenz und relative Entropie
Up: Gleichmäßig beste Tests
Previous: Neyman-Pearson-Tests
Contents
Roland Maier
2003-03-06
 Für jedes
Für jedes
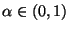 gibt es ein
gibt es ein 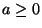 und einen
NP-Test
und einen
NP-Test 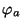 mit
mit
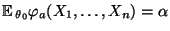 .
.
 Sei
Sei
![$ \varphi:\mathbb{R}^n\to[0,1]$](img2190.png) ein weiterer bester Test
zum Niveau
ein weiterer bester Test
zum Niveau 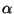 . Dann gilt
. Dann gilt
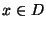 , wobei
, wobei
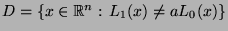 und
und 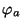 der gemäß Teilaussage
der gemäß Teilaussage 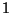 existierende
NP-Test zum Niveau
existierende
NP-Test zum Niveau 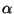 ist. Die Ausnahmemenge in
ist. Die Ausnahmemenge in 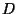 , für die
, für die
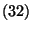 nicht gilt, hat sowohl bezüglich
nicht gilt, hat sowohl bezüglich
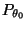 als auch bezüglich
als auch bezüglich
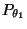 die
Wahrscheinlichkeit 0.
die
Wahrscheinlichkeit 0.