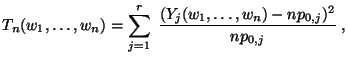- ob die erzeugten Pseudozufallszahlen als Realisierungen von gleichverteilten Zufallsvariablen aufgefasst werden können und
- ob davon ausgegangen werden kann, dass diese Zufallsvariablen unabhängig sind.
Wir betrachten zunächst den folgenden Test, um zu prüfen, ob die
Pseudozufallszahlen
![]()
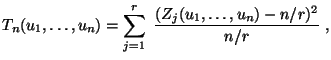
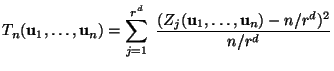
Zur Überprüfung der Güte von Zufallszahlengeneratoren gibt es noch weitere statistische Signifikanztests, durch die verifiziert werden kann,
Der zu konstruierende Signifikanztest beruht auf der
folgenden Eigenschaft der Runs
![]() .
.
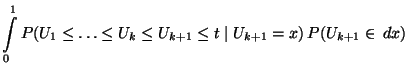 |
|||
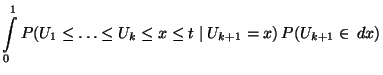 |
|||
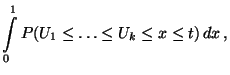 |
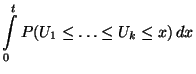 |
|||
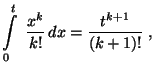 |
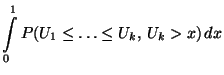 |
|||
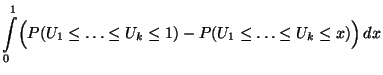 |
|||
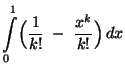 |
|||
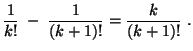 |
![$\displaystyle p_{0,j}=\sum\limits
_{k\in\mathbb{N}\cap(a_j,b_j]}\frac{k}{(k+1)!}\,,\qquad j=1,\ldots,r
$](img1215.png)