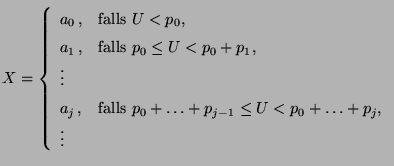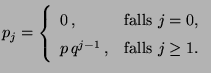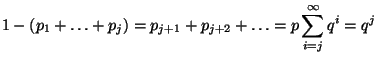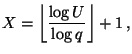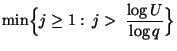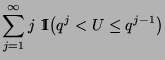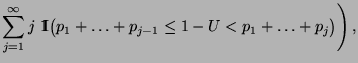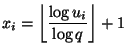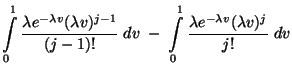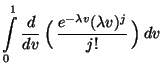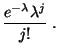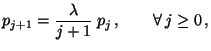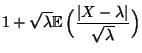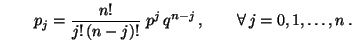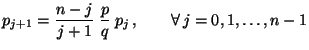Nächste Seite: Akzeptanz- und Verwerfungsmethode
Aufwärts: Transformation gleichverteilter Pseudozufallszahlen
Vorherige Seite: Inversionsmethode
Inhalt
Transformationsalgorithmen für diskrete Verteilungen
- Beispiel
 (Geometrische Verteilung)
(Geometrische Verteilung)
Für einige diskrete Verteilungen gibt es spezielle
Transformationsalgorithmen, um Pseudozufallszahlen zu erzeugen,
die als Realisierungen von Zufallsvariablen mit einer solchen
Verteilung aufgefasst werden können.
- Beispiele
-
- Poisson-Verteilung
 (mit kleinem Erwartungswert
(mit kleinem Erwartungswert 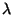 )
)
- Poisson-Verteilung
 (mit großem Erwartungswert
(mit großem Erwartungswert 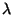 )
)
- Falls
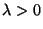 eine große Zahl ist, wobei
eine große Zahl ist, wobei 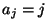 und
und
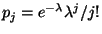 für
für
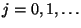 ,
,
- dann ist das unmittelbar auf dem Transformationsansatz
(13) beruhende Verfahren besser geeignet, um
Poi
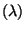 -verteilte Pseudozufallszahlen zu erzeugen,
-verteilte Pseudozufallszahlen zu erzeugen,
- wenn dabei die Gültigkeit der Ungleichungen
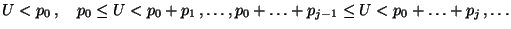 |
(18) |
in der folgenden Reihenfolge überprüft wird,
- wobei die Rekursionsformel
zur Berechnung der Summen
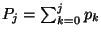 für
für 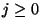 verwendet wird.
verwendet wird.
- Sei
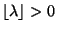 der ganzzahlige Teil von
der ganzzahlige Teil von 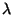 . Dann wird
zunächst geprüft, ob
. Dann wird
zunächst geprüft, ob
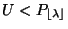 gilt.
gilt.
- Falls diese Ungleichung gilt, dann wird geprüft, ob
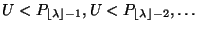 gilt, wobei in diesem
Fall
gilt, wobei in diesem
Fall
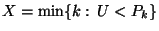 gesetzt wird.
gesetzt wird.
- Falls
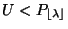 nicht gilt, dann wird geprüft, ob
nicht gilt, dann wird geprüft, ob
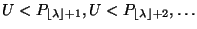 gilt, wobei erneut
gilt, wobei erneut
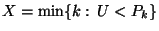 gesetzt wird.
gesetzt wird.
- Für den Erwartungswert
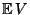 der dabei erforderlichen Anzahl
der dabei erforderlichen Anzahl 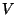 von Überprüfungen gilt dann näherungsweise, dass
von Überprüfungen gilt dann näherungsweise, dass
- wobei in der letzten Approximationsformel die Tatsache genutzt
wurde, dass die Zufallsvariable
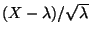 für
große
für
große 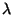 näherungsweise N
näherungsweise N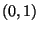 -verteilt ist,
-verteilt ist,
- was sich aus der Faltungsstabilität der Poisson-Verteilung und aus
dem zentralen Grenzwertsatz für Summen von unabhängigen und
identisch verteilten Zufallsvariablen (Theorem WR-5.16) ergibt.
- Bei dieser Vorgehensweise wächst also
- die im Mittel erforderliche Anzahl von Überprüfungen nur wie die
Quadratwurzel
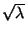 von
von 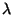 ,
,
- wogegen bei dem vorher diskutierten Verfahren zur Erzeugung
Poi
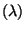 -verteilter Pseudozufallszahlen die jeweils im
Mittel erforderliche Anzahl von Standard-Pseudozufallszahlen wie
-verteilter Pseudozufallszahlen die jeweils im
Mittel erforderliche Anzahl von Standard-Pseudozufallszahlen wie
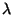 wächst.
wächst.
- Binomial-Verteilung
- Bei der Erzeugung von binomialverteilten Pseudozufallszahlen kann
man ähnlich wie im Fall der Poisson-Verteilung vorgehen.
- Für beliebige, jedoch fest vorgegebene Zahlen
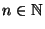 und
und
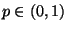 mit
mit 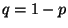 sei
sei
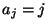
und
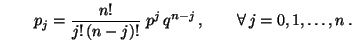
- Für
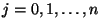 werden dann die Summen
werden dann die Summen
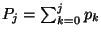 mit der Rekursionsformel
berechnet.
mit der Rekursionsformel
berechnet.
- Falls
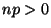 klein ist, dann wird
klein ist, dann wird
- die Gültigkeit der Ungleichungen (18) in der
natürlichen Reihenfolge überprüft,
- wobei mit
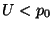 begonnen und
begonnen und
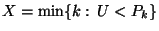 gesetzt
wird.
gesetzt
wird.
- Falls
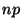 groß ist,
groß ist,
- dann ist es effizienter, die Gültigkeit der Ungleichungen
(18) in der folgenden Reihenfolge zu verifizieren.
Dabei wird zunächst geprüft, ob
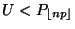 gilt.
gilt.
- Falls diese Ungleichung gilt, dann wird geprüft, ob
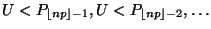 gilt, wobei in diesem Fall
gilt, wobei in diesem Fall
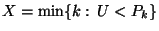 gesetzt wird.
gesetzt wird.
- Falls
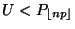 nicht gilt, dann wird geprüft, ob
nicht gilt, dann wird geprüft, ob
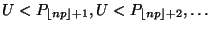 gilt, wobei erneut
gilt, wobei erneut
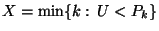 gesetzt wird.
gesetzt wird.




Nächste Seite: Akzeptanz- und Verwerfungsmethode
Aufwärts: Transformation gleichverteilter Pseudozufallszahlen
Vorherige Seite: Inversionsmethode
Inhalt
Ursa Pantle
2003-09-29
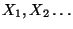 aufgefasst werden können,
aufgefasst werden können,
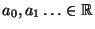 mit den
Wahrscheinlichkeiten
mit den
Wahrscheinlichkeiten
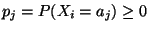 für
für
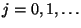 annehmen.
annehmen.
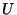 eine
eine ![$ (0,1]$](img167.png) -verteilte Zufallsvariable, und die
Zufallsvariable
-verteilte Zufallsvariable, und die
Zufallsvariable 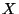 sei gegeben durch
sei gegeben durch
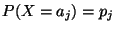 für jedes
für jedes
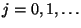 .
.
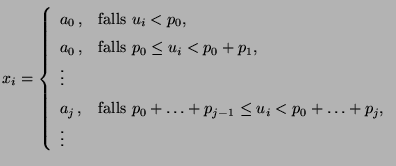
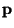 -verteilten Zufallsvariablen aufgefasst werden, wobei
-verteilten Zufallsvariablen aufgefasst werden, wobei
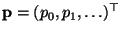 ,
,
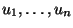 die Realisierungen von unabhängigen und im
Intervall
die Realisierungen von unabhängigen und im
Intervall ![$ (0,1]$](img167.png) gleichverteilten Zufallsvariablen
gleichverteilten Zufallsvariablen
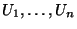 sind.
sind.