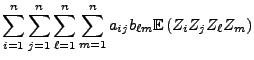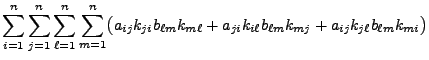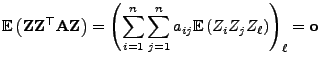Nächste Seite: Nichtzentrale -Verteilung
Aufwärts: Lineare und quadratische Formen
Vorherige Seite: Lineare und quadratische Formen
Inhalt
Definition, Erwartungswert und Kovarianz
- Definition
-
- Seien
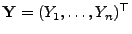 und
und
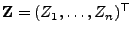 beliebige
beliebige  -dimensionale
Zufallsvektoren, und sei
-dimensionale
Zufallsvektoren, und sei
 eine symmetrische
eine symmetrische 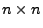 Matrix mit reellwertigen Eintragungen.
Matrix mit reellwertigen Eintragungen.
- Dann heißt die (reellwertige) Zufallsvariable
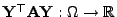 quadratische Form von
quadratische Form von
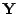 bezüglich
bezüglich
 .
.
- Die Zufallsvariable
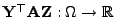 heißt bilineare Form von
heißt bilineare Form von
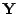 und
und
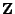 bezüglich
bezüglich
 .
.
Zunächst bestimmen wir den Erwartungswert von quadratischen bzw.
bilinearen Formen.
Theorem 1.5

Seien
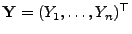
und
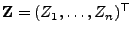
beliebige

-dimensionale
Zufallsvektoren, und sei

eine symmetrische
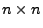
Matrix mit reellwertigen Eintragungen. Die Erwartungswertvektoren
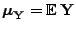
und
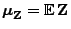
sowie die
Kovarianzmatrizen
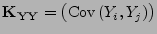
und
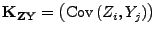
seien
wohldefiniert. Dann gilt
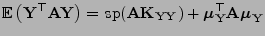 und und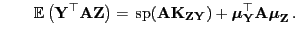 |
(26) |
- Beweis
-
Auf ähnliche Weise lässt sich eine Formel für die Kovarianz von
quadratischen Formen normalverteilter Zufallsvektoren herleiten.
Dabei sind die folgenden Formeln für die dritten bzw. vierten
gemischten Momente der Komponenten von zentrierten
normalverteilten Zufallsvektoren nützlich.
Lemma 1.11
Sei
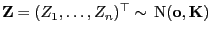
ein
normalverteilter Zufallsvektor mit Erwartungswertvektor
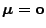
und mit beliebiger
Kovarianzmatrix
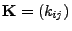
. Dann gilt
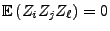 und und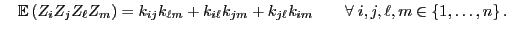 |
(27) |
Der Beweis von Lemma 1.11 wird hier weggelassen
und in den Übungen diskutiert, vgl. Übungsaufgabe 2.3.
- Beweis
-
Wir leiten nun noch die folgende Formel für den Kovarianzvektor
von linearen bzw. quadratischen Formen normalverteilter
Zufallsvektoren her.
Theorem 1.7

Sei
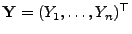
ein

-dimensionaler
Zufallsvektor mit
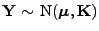
, und seien
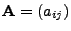
,
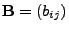
beliebige symmetrische
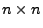
Matrizen. Dann gilt
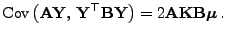 |
(30) |
- Beweis
-
- Weil
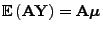 und weil in
Theorem 1.5 gezeigt wurde, dass
ergibt sich, dass
und weil in
Theorem 1.5 gezeigt wurde, dass
ergibt sich, dass
- Außerdem gilt
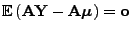 , und aus
(29) folgt mit
, und aus
(29) folgt mit
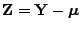 , dass
, dass
- Somit ergibt sich, dass





Nächste Seite: Nichtzentrale -Verteilung
Aufwärts: Lineare und quadratische Formen
Vorherige Seite: Lineare und quadratische Formen
Inhalt
Hendrik Schmidt
2006-02-27
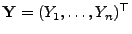 und
und
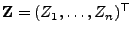 beliebige
beliebige  -dimensionale
Zufallsvektoren, und sei
-dimensionale
Zufallsvektoren, und sei
 eine symmetrische
eine symmetrische 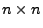 Matrix mit reellwertigen Eintragungen.
Matrix mit reellwertigen Eintragungen.
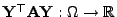 quadratische Form von
quadratische Form von
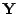 bezüglich
bezüglich
 .
.
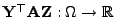 heißt bilineare Form von
heißt bilineare Form von
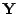 und
und
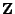 bezüglich
bezüglich
 .
.