



Nächste Seite: Konfidenzbereiche; Prognose von Zielvariablen
Aufwärts: Normalverteilte Störgrößen
Vorherige Seite: Verteilungs- und Unabhängigkeitseigenschaften von
Inhalt
Tests für die Regressionskoeffizienten;
Quadratsummenzerlegung
Zunächst diskutieren wir den folgenden F-Test, der auch Test
auf Gesamtzusammenhang bzw. Test auf Signifikanz des
Modells genannt wird.
- Hierbei wird die Null-Hypothese
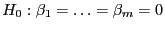 (gegen die Alternative
(gegen die Alternative
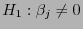 für ein
für ein
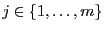 ) getestet.
) getestet.
- Die Wahl der Testgröße ist durch die folgende Quadratsummenzerlegung motiviert.
- Beweis
-
- Es gilt
- Dabei ergibt sich die vorletzte Gleichheit aus der folgenden
Überlegung: Es gilt

- Beachte
-
Aus unserer Modellannahme, dass die Designmatrix
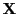 vollen
Rang hat, d.h.
vollen
Rang hat, d.h.
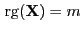 , ergibt sich die Ungleichung
, ergibt sich die Ungleichung
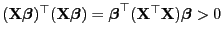 , wenn die Hypothese
, wenn die Hypothese
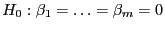 falsch ist.
falsch ist.
Um einen auf
 basierenden Test der Hypothese
basierenden Test der Hypothese
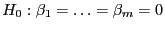 konstruieren zu können, muss die
Verteilung der Testgröße
konstruieren zu können, muss die
Verteilung der Testgröße
 bestimmt werden.
bestimmt werden.
Theorem 2.10

Unter
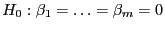
gilt
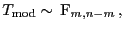 |
(45) |
d.h., die in
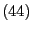
gegebene Testgröße

ist
F-verteilt mit
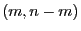
Freiheitsgraden.
- Beweis
-
- Unter
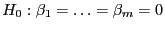 gilt
gilt
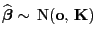 mit
mit
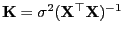 .
.
- Hieraus folgt, dass
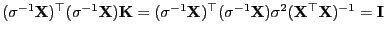 , d.h. insbesondere, dass die Matrix
, d.h. insbesondere, dass die Matrix
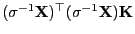 idempotent ist.
idempotent ist.
- Aus Theorem 1.9 ergibt sich nun, dass die
quadratische Form
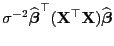 eine (zentrale)
eine (zentrale)  -Verteilung mit
-Verteilung mit 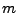 Freiheitsgraden hat.
Freiheitsgraden hat.
- Außerdem hatten wir in Theorem 2.7 gezeigt, dass die
Zufallsvariable
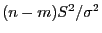 eine (zentrale)
eine (zentrale)
 -Verteilung mit
-Verteilung mit 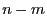 Freiheitsgraden hat.
Freiheitsgraden hat.
- In Theorem 2.8 hatten wir gezeigt, dass
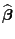 und
und 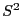 unabhängig sind.
unabhängig sind.
- Aus dem Transformationssatz für unabhängige Zufallsvektoren (vgl.
Theorem I-1.8) folgt somit, dass auch die Zufallsvariablen
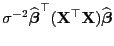 und
und
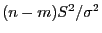 unabhängig sind.
unabhängig sind.
- Die Behauptung ergibt sich nun aus der Definition der
F-Verteilung, vgl. Abschnitt I-3.1.3.

- Beachte
-
Zur Verifizierung von Hypothesen über einzelne Komponenten
von
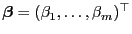 werden dagegen
t-Tests verwendet.
werden dagegen
t-Tests verwendet.
- Beachte
-
Die bisher in diesem Abschnitt betrachteten Tests sind
Spezialfälle des folgenden universellen Tests. Dabei wird
ein beliebiger Teil der Komponenten des Parametervektors
 getestet.
getestet.
Wir diskutieren nun noch einen allgemeinen Test für
Linearformen des Parametervektors
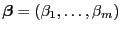 .
.
Theorem 2.11

Unter
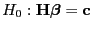
gilt
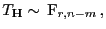 |
(58) |
d.h., die in
gegebene Testgröße
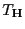
ist
F-verteilt mit
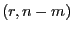
Freiheitsgraden.
- Beweis
-
- Beachte
 Die Nullhypothese
Die Nullhypothese
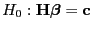 wird abgelehnt, wenn
wird abgelehnt, wenn
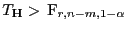 , wobei
, wobei
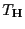 die in
die in
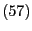 gegebene Testgröße ist.
gegebene Testgröße ist.




Nächste Seite: Konfidenzbereiche; Prognose von Zielvariablen
Aufwärts: Normalverteilte Störgrößen
Vorherige Seite: Verteilungs- und Unabhängigkeitseigenschaften von
Inhalt
Hendrik Schmidt
2006-02-27
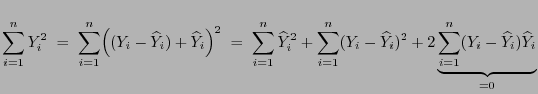
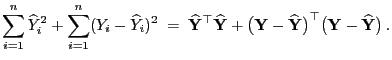
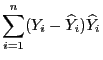
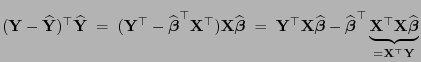
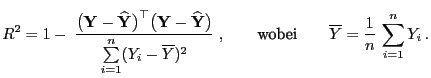
![]() vollen
Rang hat, d.h.
vollen
Rang hat, d.h.
![]() , ergibt sich die Ungleichung
, ergibt sich die Ungleichung
![]() , wenn die Hypothese
, wenn die Hypothese
![]() falsch ist.
falsch ist.
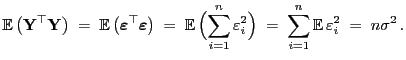
![]() basierenden Test der Hypothese
basierenden Test der Hypothese
![]() konstruieren zu können, muss die
Verteilung der Testgröße
konstruieren zu können, muss die
Verteilung der Testgröße
![]() bestimmt werden.
bestimmt werden.
![]() werden dagegen
t-Tests verwendet.
werden dagegen
t-Tests verwendet.
![]() getestet.
getestet.
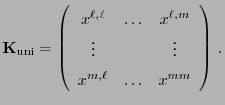
![]() .
.