Crash Course in SystemVerilog: Sequential Logic

In the lecture, we've seen that circuits with flip-flops require consideration of clock signal edges in their mathematical descriptions. This can be achieved by describing a sequence of logical states. For example, with the equations (initial value of ) and (value of after a rising edge), the following circuit with a flip-flop and an inverter can be described:

In SystemVerilog, this can be described as follows:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

module Example3 (
    input logic clock,
    output logic Q
);

    initial begin
        Q = 0;
    end

    always_ff @ (posedge clock) begin
        Q <= ~Q;
    end

endmodule

The initial value is set in the “initial” block, and how the state of Q changes after a rising edge is described in the always_ff block (ff stands for Flip-Flop).

Of course, SystemVerilog allows expressing that a circuit consists of both logic gates and flip-flops, and accordingly, it can be described with both combinatorial and sequential logic. For example, this circuit

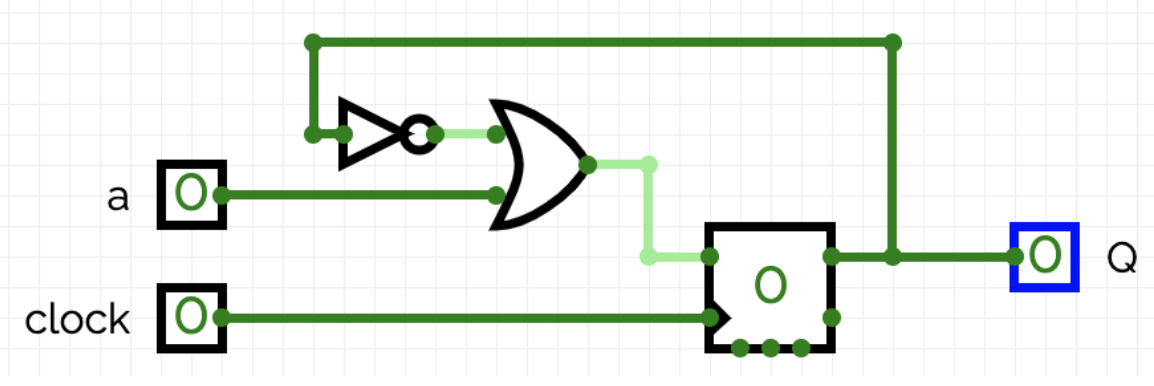
can be described by the following SystemVerilog code:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

module test (
    input logic a,
    input logic clock,
    output logic Q
);

    logic nextQ;

    initial begin
        Q = 0;
    end

    always_comb begin
        nextQ = ~Q | a;
    end

    always_ff @ (posedge clock) begin
        Q <= nextQ;
    end

endmodule